
I. Keplers Beziehung zu Galilei
Johannes Kepler und der sieben Jahre ältere Galileo Galilei bewirkten zusammen einen Umbruch auf dem Gebiet der Wissenschaften, dementsprechend hatten sie in ihren wissenschaftlichen Ansichten und ihrer Art auch gewisse Gemeinsamkeiten:  Beide vertraten das heliozentrische Weltsystem des Nikolaus Kopernikus und waren bestrebt dieses weiterzuentwickeln und zu beweisen. So schrieb Galilei in einem Brief an Kepler aus dem Jahre 1597: „…unser Lehrer Kopernikus, der verlacht wurde".
Beide vertraten das heliozentrische Weltsystem des Nikolaus Kopernikus und waren bestrebt dieses weiterzuentwickeln und zu beweisen. So schrieb Galilei in einem Brief an Kepler aus dem Jahre 1597: „…unser Lehrer Kopernikus, der verlacht wurde".
Außerdem waren beide sehr gläubige Menschen, deren Wissenschaft nicht gegen die Kirche beziehungsweise Gott sein sollte, sondern diesen und seine Welt ehren sollte. Sie waren also keine „Rebellen“, sondern sahen sich viel mehr als „Forscher in Gottes Sinn“. Ihre Intension war es nicht die Kirche zu widerlegen oder zu spalten, sondern vielmehr war ihnen an einer Reform der Weltsicht der Kirche gelegen. Doch beide wurden von kirchlicher Seite missverstanden und ihre Werke nicht geachtet.
Doch trotz allem waren sich die Beiden in ihren Eigenschaften und ihrer Persönlichkeit recht unterschiedlich.
So funktionierte die Zusammenarbeit Keplers und Galileis nicht reibungslos und auch der gemeinsame Briefwechsel wurde im Jahre 1610 von Seite Galileis abgebrochen, als er auf mindestens sechs Briefe des Deutschen nicht mehr antwortete (bis auf eine kurze Empfehlung im Jahre 1627).
Verdeutlicht wird dieses unharmonische Verhältnis schon zu Beginn des Kontaktes, als Keplers Mysterium Cosmograhicum erschien:
Kepler schickte ein Exemplar an den Kollegen aus Italien – der bisher noch keinen Namen als Astronom hatte, sondern nur als Physiker bekannt war – und war hoch erfreut über dessen höfliche Antwort, in der sich Galilei zur Lehre des Kopernikus bekannte aber auch seine Zweifel, öffentlich dafür einzutreten. Daraufhin antworte Kepler dem neuen, wie Galilei schrieb, „aufrichtigen Freund“ voller Vorfreude auf einen zukünftigen regen Gedankenaustausch: „Seid guten Mutes, Galilei, und tretet hervor. Wenn ich recht vermute gibt es unter den bedeutenden Mathematikern Europas wenige, die sich von uns scheiden wollen. So groß ist die Macht der Wahrheit. [...] Nun möchte ich noch eine Beobachtung von euch Euch erbitten; da ich nämlich keine Instrumente besitze, muß ich zu anderen meine Zuflucht nehmen.“ Kepler bat hier um Beobachtungen bezüglich der Entfernung der Fixsternsphäre. Doch zu seiner großen Enttäuschung erhielt er nie eine Antwort auf diesen Brief.
Und auch im weiteren Verlauf der Beziehung verhielt sich Galilei Kepler gegenüber wenig kollegial. Später erfuhr er sogar, dass Galilei einige Entdeckungen Keplers als seine eigenen ausgebe. Doch Kepler reagierte darauf selbstlos und meinte: „Galilei halte ich mitnichten zurück, meine Sachen für sich in Anspruch zu nehmen. Meine Zeugen sind das helle Tageslicht und die Zeit. Wer auf diese Zeugen hört – die Gebildeten und Vernünftigen hören darauf –, der lässt sich nie täuschen.“
Und hierin zeigt sich auch ein weiterer Unterschied in der Persönlichkeit der beiden Wissenschaftler: Während Kepler ein bescheidener und friedlicher Mann war, der nach Anerkennung für die Sache (also seine Entdeckungen) strebte, war Galilei sehr darauf bedacht selbst Anerkennung und Ruhm zu erlangen und ließ sich gerne auf die eine oder andere Auseinandersetzung ein. Somit sah zunächst Kepler in Galilei eher einen Gleichgesinnten mit dem er sich hätte austauschen können, Galilei in Kepler aber eher einen Rivalen, der seinen eigenen Ruhm schmälern könnte oder der mit seiner Hilfe selbst zu unverdienter Anerkennung kommen könnte.
 Bezeichnend hierfür ist auch, dass Galilei sich nicht bereiterklärte, Kepler eines seiner neu entwickelten Fernrohre zukommen zu lassen, als dieser ihn darum bat. Galilei antwortete auf Keplers Bitte, er wolle in Zukunft neue Instrumente bauen und sie seinen Freunden schicken. Zu welchen er Kepler anscheinend nicht zählte, denn der deutsche Astronom erhielt nie ein solches.
Bezeichnend hierfür ist auch, dass Galilei sich nicht bereiterklärte, Kepler eines seiner neu entwickelten Fernrohre zukommen zu lassen, als dieser ihn darum bat. Galilei antwortete auf Keplers Bitte, er wolle in Zukunft neue Instrumente bauen und sie seinen Freunden schicken. Zu welchen er Kepler anscheinend nicht zählte, denn der deutsche Astronom erhielt nie ein solches.
Zuvor hatte Kepler Galileis, von der Fachwelt wenig gepriesene, „Sidereus nuncius“ (Sternenbote/-botschaft) in einem offenen Brief durchaus gelobt und stand Galilei damit zur Seite. Wobei er aber in seiner Vorrede anmerkte: „...Auch glaube ich nicht, dass sich der Italiener Galilei um mich - den Deutschen - so sehr verdient gemacht hat, dass ich ihm dafür schmeicheln müsste, indem ich die Wahrheit und meine innerste Überzeugung nach ihm einrichte.
Zudem sollte niemand glauben, dass meine freimütige Zustimmung zu Galilei anderen die Freiheit nimmt, anders zu denken. Ich lobte ihn ohne die Rücksicht auf das Urteil irgendeines anderen.“
Ein Treffen der beiden großen Wissenschaftler fand übrigens nie statt.
 Der italienische Mathematiker, Physiker und Philosoph wurde am 15. Februar 1564 in Pisa geboren. Er war der Sohn eines wenig begüterten florentinischen Tuchhändlers, Musikers und Musiktheoretikers, der seinerseits „musik-physikalische“ Untersuchungen anstellte.
Der italienische Mathematiker, Physiker und Philosoph wurde am 15. Februar 1564 in Pisa geboren. Er war der Sohn eines wenig begüterten florentinischen Tuchhändlers, Musikers und Musiktheoretikers, der seinerseits „musik-physikalische“ Untersuchungen anstellte.
Der kleine Galilei, der später sagte er habe mit dem Gedanken gespielt, Maler zu werden, wurde zunächst in einem Kloster (Vallombroso) als Novize erzogen, bevor er ab 1581 auf Wunsch seines Vaters ein Medizinstudium an der Universität Pisas begann. Doch nach drei oder vier Jahren des Medizin- und Philosophiestudiums entschied er sich für einen Wechsel und studierte von nun an die mehr in seinem Interesse stehenden Fächer der Naturwissenschaften und Mathematik. Er beendete das Studium ohne Abschluss und ging 1985 nach Florenz um seine Studien privat fortzusetzen.
Als 26-Jähriger wurde Galilei, der sich lange mit den Schriften des Aristoteles beschäftigt hatte, auf Grund seiner guten Beziehungen zum Professor der Mathematik in Pisa ernannt. Die Stelle wurde jedoch nicht sehr gut vergütet und so bekam Galilei, als 1591 sein Vater starb und er dadurch für Mutter, drei jüngere Geschwister und die Mitgift der älteren Schwester aufkommen musste, finanzielle Probleme. Aus diesem Grund ging er im darauffolgenden Jahr als Professor für Mathematik und Physik nach Padua, was eine etwas besser besoldete Stelle darstellte. Nebenbei gab er noch – aus demselben Grund – Privatunterricht an einige Schüler aus begütertem Elternhaus.
Ein weiterer Aufstieg wurde Galilei, der inzwischen schon einige nennenswerte Entdeckungen gemacht hatte, im Jahre 1610 ermöglicht, indem er als Hofmathematiker des Großherzogs von Florenz Cosimo de Medici (sein ehemaliger Schüler) in Florenz angestellt wurde. Hierdurch erhoffte sich Galilei neben einer besseren Bezahlung auch mehr Zeit und Freiheit für seine Experimente. Gleichzeitig trennte er sich aber auch von seiner Haushälterin Marina Gamba, mit der er elf Jahre lang eine Beziehung geführt und drei Kinder hatte, die in den Jahren 1600, 1601 und 1606 zur Welt kamen.
1611 reiste Galilei erstmals nach Rom, mit der Absicht die kirchliche Oberbehörde von der Richtigkeit des kopernikanischen Weltbildes zu überzeugen, was ihm aber nicht gelang.
In der Folgezeit nutzte er die ihm gegebenen Möglichkeiten, indem er weitere Experimente anstellte und seine Ergebnisse und Gedanken veröffentlichte.
 1632 erscheint das Werk, das Galilei zum Verhängnis werden sollte: Dialogo di Galileo Galilei sopra i due Massimi Sistemi del Mondo Tolemaico e Copernicano (Dialog über die zwei wichtigsten Weltsysteme, das Ptolemäische und das Kopernikanische).
1632 erscheint das Werk, das Galilei zum Verhängnis werden sollte: Dialogo di Galileo Galilei sopra i due Massimi Sistemi del Mondo Tolemaico e Copernicano (Dialog über die zwei wichtigsten Weltsysteme, das Ptolemäische und das Kopernikanische).
Nachdem Galileis Versuche, die Kirche zu überzeugen bisher fehlgeschlagen waren, erhoffte er sich neue Chancen bei dem 1618 neu eingesetzten Papst Urban VIII. Da sein erstes Werk „Il Saggiatore“ („Prüfer mit der Goldwaage“) keine Beachtung fand, veröffentlichte Galilei eben 1632 dieses Buch, mit dem er die Menschen auf eine besondere Art und Weise vom neuen Weltbild überzeugen wollte: Er lies einen Vertreter des Ptolemäischen und einen des Kopernikanischen Weltsystems miteinander diskutieren, wobei der Vertreter des Kopernikanischen schlussendlich die deutlich besseren Argumente anführt und somit gewinnt. Diese Diskussion wurde von den Offiziellen des Vatikans nicht mehr für eine hypothetische Schreibweise gehalten und sie verhängten deshalb ein Druckverbot. Kurz darauf wurde der Fall der Inquisition übergeben und Galilei wurde zum Papst nach Rom bestellt. Auf Grund gesundheitlicher Probleme verzögerte sich seine Reise noch etwas, bis er schließlich im April 1633 offiziell vernommen wurde. Der nun begonnene Prozess, während dessen Galilei auch einige Tage ein Apartment der Inquisition beziehen musste, endete am 22. Juni 1633 mit dem Widerruf der Theorie des 69-Jährigen. Unter Androhung der Folter verlies Galilei vor den Kardinälen kniend folgenden Text, der ihm von der Inquisition vorbereitet worden war:
„Ich, Galileo Sohn des Vinzenz Galilei aus Florenz, siebzig Jahre alt, stand persönlich vor Gericht und ich kniete vor Euch Eminenzen, die Ihr in der ganzen Christenheit die Inquisitionen gegen die ketzerische Verworfenheit seid. Ich habe vor mir die heiligen Evangelien, berühre sie mit de Hand und schwöre, dass ich immer geglaubt habe, auch jetzt glaube und mit Gottes Hilfe auch in Zukunft glauben werde, alles was die heilige katholische und apostolische Kirche für wahr hält, predigt und lehrt.Es war mir von diesem Heiligen Offizium von Rechts wegen die Vorschrift auferlegt worden, dass ich völlig die falsche Meinung aufgeben müsse, dass die Sonne der Mittelpunkt der Welt ist, und dass sie sich nicht bewegt, und dass die Erde nicht der Mittelpunkt der Welt ist, und dass sie sich bewegt. Es war mir weiter befohlen worden, dass ich diese falsche Lehre nicht vertreten dürfe, sie nicht verteidigen dürfe und dass ich sie in keiner Weise lehren dürfe, weder in Wort noch in Schrift. Es war mir auch erklärt worden, dass jene Lehre der Heiligen Schrift zuwider sei.  Trotzdem habe ich ein Buch geschrieben und zum Druck gebracht, in dem ich jene bereits verurteilte Lehre behandele und in dem ich mit viel Geschick Gründe zugunsten derselben beibringe, ohne jedoch zu irgendeiner Entscheidung zu gelangen. Daher bin ich der Ketzerei in hohem Maße verdächtig befunden worden, darin bestehend, dass ich die Meinung vertreten und geglaubt habe, dass die Sonne Mittelpunkt der Welt und unbeweglich ist, und dass die Erde nicht Mittelpunkt ist und sich bewegt. Ich möchte mich nun vor Euren Eminenzen und vor jedem gläubigen Christen von jenem schweren Verdacht, den ich gerade näher bezeichnete, reinigen. Daher schwöre ich mit aufrichtigem Sinn und ohne Heuchelei ab, verwünsche und verfluche jene Irrtümer und Ketzereien und darüber hinaus ganz allgemein jeden irgendwie gearteten Irrtum, Ketzerei oder Sektiererei, die der Heiligen Kirche entgegen ist. Ich schwöre, dass ich in Zukunft weder in Wort noch in Schrift etwas verkünden werde, das mich in einen solchen Verdacht bringen könnte. Wenn ich aber einen Ketzer kenne, oder jemanden der Ketzerei verdächtig weiß, so werde ich ihn diesem Heiligen Offizium anzeigen oder ihn dem Inquisitor oder der kirchlichen Behörde meines Aufenthaltortes angeben.
Trotzdem habe ich ein Buch geschrieben und zum Druck gebracht, in dem ich jene bereits verurteilte Lehre behandele und in dem ich mit viel Geschick Gründe zugunsten derselben beibringe, ohne jedoch zu irgendeiner Entscheidung zu gelangen. Daher bin ich der Ketzerei in hohem Maße verdächtig befunden worden, darin bestehend, dass ich die Meinung vertreten und geglaubt habe, dass die Sonne Mittelpunkt der Welt und unbeweglich ist, und dass die Erde nicht Mittelpunkt ist und sich bewegt. Ich möchte mich nun vor Euren Eminenzen und vor jedem gläubigen Christen von jenem schweren Verdacht, den ich gerade näher bezeichnete, reinigen. Daher schwöre ich mit aufrichtigem Sinn und ohne Heuchelei ab, verwünsche und verfluche jene Irrtümer und Ketzereien und darüber hinaus ganz allgemein jeden irgendwie gearteten Irrtum, Ketzerei oder Sektiererei, die der Heiligen Kirche entgegen ist. Ich schwöre, dass ich in Zukunft weder in Wort noch in Schrift etwas verkünden werde, das mich in einen solchen Verdacht bringen könnte. Wenn ich aber einen Ketzer kenne, oder jemanden der Ketzerei verdächtig weiß, so werde ich ihn diesem Heiligen Offizium anzeigen oder ihn dem Inquisitor oder der kirchlichen Behörde meines Aufenthaltortes angeben.
Ich schwöre auch, dass ich alle Bußen, die mir das Heilige Offizium auferlegt hat oder noch auferlegen wird, genauestens beachten und erfüllen werde. Sollte ich irgendeinem meiner Versprechen und Eide, was Gott verhüten möge, zuwiderhandeln, so unterwerfe ich mich allen Strafen und Züchtigungen, die das kanonische Recht und andere allgemeine und besonders einschlägige Bestimmungen gegen solche Sünder festsetzen und verkünden. Dass Gott mir helfe und seine heiligen Evangelien, die ich mit den Händen berühre.
Ich, Galileo Galilei, habe abgeschworen, geschworen, versprochen und mich verpflichtet, wie ich eben näher ausführte. Zum Zeugnis der Wahrheit habe ich diese Urkunde meines Abschwörens eigenhändig unterschrieben und sie Wort für Wort verlesen, in Rom im Kloster der Minerva am 22. Juni 1633. Ich Galileo Galilei, habe abgeschworen und eigenhändig unterzeichnet.“
Der Legende nach soll Galilei, der an seiner Überzeugung festhielt, beim Verlassen des Gerichtssaals folgende Worte gemurmelt haben: „Eppur si muove" („Und sie [die Erde] bewegt sich doch").
Galilei wurde zu unbefristeter Haft in seinem Landhaus in Arcetri bei Florenz verurteilt. Diese „unbefristete Haft“ bedeutetet Hausarrest und das Verbot jeglicher Lehrtätigkeit. Nicht einmal ein Arztbesuch war ihm gestattet.
Galilei blieb also bis zu seinem Tode ein Gefangener der Inquisition.
1637 erblindete der schon immer unter Sehschwächen leidende Galilei vollständig auf beiden Augen. Man vermutet, dass dies eine Folge seiner anfangs ohne ausreichenden Schutz unternommenen Sonnenbeobachtungen war.  (Auch dieses Augenleiden hatte Galilei mit Kepler gemein.)
(Auch dieses Augenleiden hatte Galilei mit Kepler gemein.)
Am 8. Januar 1642 starb Galileo Galilei in Arcetri. Ein feierliches Begräbnis in einem ehren- und prunkvollen Grab, das der Großherzog vorgesehen hatte, wurde dem italienischen Wissenschaftler jedoch verwehrt.
Doch hiermit war der Fall Galilei noch nicht abgeschlossen. Neben seinem Ansehen, das er in der Wissenschaft genießt, befasste sich auch die katholische Kirche noch einmal mit dem einstigen „Ketzer“. 1979 beauftragte Papst Johannes Paul II. die Päpstliche Akademie der Wissenschaft, den berühmten Fall aufzuarbeiten.
Am 31. Oktober 1992 hielt Johannes Paul II. eine Rede, die zum einen als Entschuldigung und zum anderen als Heilung des gegenseitigen Missverstehens von Wissenschaft und Kirche gesehen wird.
Am 2. November 1992 wurde Galileo Galilei schließlich formal von der römisch-katholischen Kirche rehabilitiert.
III. Seine Erkenntnisse und Erfindungen
Galileo Galilei entdeckte und erkannte zahlreiche naturwissenschaftliche Dinge in den Gebieten der Mathematik, Physik und Astronomie. Seine wahren Leistungen waren aber eigentlich gar nicht nur seine Entdeckungen, mindestens genauso wichtig für alle, die ihm folgten war Galileis Weg zu Erkenntnissen zu gelangen.  So war das revolutionäre an seiner Arbeit zum einen seine Art der Forschung und zum anderen seine Art der Ergebnisse; seine Vorgehensweise war neuartig: Galilei entdeckte dass Experiment als wesentliches Mittel zur Erkenntnis von Gesetzmäßigkeiten der Natur. Seine Fragen stellte er daraufhin an das Experiment, seinen Verlauf und sein Ergebnis und nicht an die reine menschliche Vernunft oder den menschlichen Glauben. Die Wissenschaftler vor ihm – besonders auch Aristoteles – fragten stets nach dem „warum“ eines physikalischen Vorgangs; Galilei aber fragte nun nach dem „wie“ eines Prozesses. Außerdem war Galilei der erste, der die Gesetze der Physik in mathematische Formeln umsetzte. Dementsprechend sagt man er habe Folgendes als sein Forschungsprinzip angegeben:
So war das revolutionäre an seiner Arbeit zum einen seine Art der Forschung und zum anderen seine Art der Ergebnisse; seine Vorgehensweise war neuartig: Galilei entdeckte dass Experiment als wesentliches Mittel zur Erkenntnis von Gesetzmäßigkeiten der Natur. Seine Fragen stellte er daraufhin an das Experiment, seinen Verlauf und sein Ergebnis und nicht an die reine menschliche Vernunft oder den menschlichen Glauben. Die Wissenschaftler vor ihm – besonders auch Aristoteles – fragten stets nach dem „warum“ eines physikalischen Vorgangs; Galilei aber fragte nun nach dem „wie“ eines Prozesses. Außerdem war Galilei der erste, der die Gesetze der Physik in mathematische Formeln umsetzte. Dementsprechend sagt man er habe Folgendes als sein Forschungsprinzip angegeben:
„Wer wissenschaftliche Fragen ohne Hilfe der Mathematik lösen will, unternimmt Undurchführbares. Man muß messen, was messbar ist, und messbar machen, was noch nicht messbar ist.“
Somit nennt man ihn heute sowohl den „Begründer des experimentellen Denkens aller Naturwissenschaftler“, als auch den „Vater der klassischen Physik“, denn er leitete mit seiner Art der Forschung ein neues Zeitalter der Wissenschaft ein.
Was ebenfalls neu war an Galilei, war seine Darstellungsweise: er war einer der ersten Italiener, der seine Forschungsergebnisse fast ausschließlich in seiner Muttersprache darstellte. Zuvor wurde Latein als Sprache der Gelehrten verwendet, wodurch dem „einfachen“ Volk nicht möglich war, die Lehren zu verfolgen oder gar zu beginnen unliebsame Fragen zu stellen. Galilei aber wollte das Volk miteinbeziehen und in gewisser Form vom richtigen Verständnis und Wissen überzeugen. So bereitete er seine Forschungsergebnisse in leicht verständlichen Dialogen aber gleichzeitig in vorbildlich schönem, stilvollen Italienisch auf.
Galileis Erkenntnisse, Entdeckungen und Entwicklungen:
- Widerlegung der aristotelischen Lehrmeinung zur Fallgeschwindigkeit:
 Laut Aristoteles sei die Fallgeschwindigkeit proportional zum Gewicht eines Körpers. Galilei aber zeigt, dass verschieden schwere Kugeln gleich schnell fallen. Man sagt er habe dies mit Hilfe eines Experiments am Schiefen Turm von Pisa demonstriert: Er soll vor Augen seiner Studenten zwei unterschiedlich schwere Körper herunterfallen lassen haben. In Galileis Schriften und Manuskripten findet sich jedoch kein Hinweis auf solche Versuche, was mangels hinreichend genauer Uhren quantitativ ohnehin so gut wie nicht auswertbar gewesen wäre.
Laut Aristoteles sei die Fallgeschwindigkeit proportional zum Gewicht eines Körpers. Galilei aber zeigt, dass verschieden schwere Kugeln gleich schnell fallen. Man sagt er habe dies mit Hilfe eines Experiments am Schiefen Turm von Pisa demonstriert: Er soll vor Augen seiner Studenten zwei unterschiedlich schwere Körper herunterfallen lassen haben. In Galileis Schriften und Manuskripten findet sich jedoch kein Hinweis auf solche Versuche, was mangels hinreichend genauer Uhren quantitativ ohnehin so gut wie nicht auswertbar gewesen wäre.
Seinen Ergebnissen wurde aber von Seiten der Gelehrten keine Beachtung geschenkt. Man war der Auffassung ein solch junger und wohl noch unerfahrener Mann – er war gerade 26 Jahre alt – habe nicht an den Fundamenten der Wissenschaft zu rütteln.
- Entdeckung der Pendelgesetze:
Er fand heraus, dass die Dauer einer Pendelschwingung mit einer bestimmten Pendellänge unabhängig von der Bogenlänge oder Amplitude immer gleich lang ist (nur wenn die Amplitude sehr groß wird, hängt die Schwingungsdauer des Pendels von der Amplitude ab). Es bestimmt also nur die Länge des Pendels die Schwingungsdauer. Galileo erkannte die Bedeutung dieser als Isochronie bezeichneten Erscheinung für die Zeitmessung und beschäftigte sich sein Leben lang mit der Frage, wie man diese Entdeckung zur Konstruktion einer Pendeluhr nutzen könne.
- Entdeckung der Fall- und Trägheitsgesetze:
Diese Gesetze stellen das eigentliche Hauptwerk Galileis dar. Er erschuf sie während seiner Zeit auf dem Landgut Arceti und veröffentlicht sie außerhalb der Landesgrenzen in dem Buch „Discorsi e dimonstrationi matematiche" (er ließ es nach Holland schmuggeln). Galilei stellte fest, dass ein Stein beim Fallen erst ganz langsam ist und dann immer schneller wird. Da er nicht bestätigen kann, dass die Geschwindigkeit in gleichen Wegabschnitten um gleiche Beträge wächst, schlussfolgert er, dass seine Annahme, die Geschwindigkeit sei proportional zu den Zeitabschnitten, richtig ist. Daraus ergab sich v = a t (aus der Ruhelage heraus). Auf Grund seiner Annahme, die Durchschnittsgeschwindigkeit betröge ½ a t, ergab sich somit für den Weg s = ½ a t t; er wächst also mit dem Quadrat der Zeit. Hiermit entdeckte Galilei also die Beschleunigung und die Tatsache, dass diese etwas von der Geschwindigkeit völlig verschiedenes ist.
Galilei stellte fest, dass ein Stein beim Fallen erst ganz langsam ist und dann immer schneller wird. Da er nicht bestätigen kann, dass die Geschwindigkeit in gleichen Wegabschnitten um gleiche Beträge wächst, schlussfolgert er, dass seine Annahme, die Geschwindigkeit sei proportional zu den Zeitabschnitten, richtig ist. Daraus ergab sich v = a t (aus der Ruhelage heraus). Auf Grund seiner Annahme, die Durchschnittsgeschwindigkeit betröge ½ a t, ergab sich somit für den Weg s = ½ a t t; er wächst also mit dem Quadrat der Zeit. Hiermit entdeckte Galilei also die Beschleunigung und die Tatsache, dass diese etwas von der Geschwindigkeit völlig verschiedenes ist.
Zur Untersuchung dieser Gesetze, führte Galilei als Versuchsanordnung die schiefe Ebene mit Kugeln aus verschiedenen Materialien ein. Somit war es erstmals möglich, die Geschwindigkeit der langsam anrollenden Kugeln zu messen. So stellte er fest, dass auch die Geschwindigkeit auf schiefen Ebenen zunimmt.
- Entdeckungen zur heutigen Elastizitätstheorie:
Auch wenn Galilei noch keine quantitative Theorie aufstellen konnte, entdeckte er, dass die Tragfähigkeit eines Balkens größer ist, wenn man ihn hochkant, nicht flachkant stellt und war der Erste, der die äußere Belastung in Relation zu den inneren Spannungen setzte.
- Erkenntnisse zur bogenförmigen Bewegung eines Geschosses:
Galilei wies nach, dass diese Bewegung aus zwei Komponenten besteht. So stellte er fest, dass hier eine von der Trägheit bestimmte horizontale und eine von stetiger Beschleunigung bestimmte nach unten gerichtete Komponente zusammenwirken. Daraus ergibt sich dann die parabelförmige Flugbahn.
- Bestimmung des Gewichtes von Luft:
Galilei widerlegte 1614 die bisher vorherrschende Meinung von gewichtsloser Luft und bestimmte ihr spezifisches Gewicht als ein 600stel des Gewichts von Wasser. Auch hiermit entkräftete er eine aristotelische Anschauung.
- Erbauung eines leistungsstarken Fernrohres und in dessen Folge zahlreiche Entdeckungen am Himmel:
 Er baute mit Hilfe seiner erlernten Schleifkunst aus Brillenlinsen – nach dem Vorbild des in Holland von Jan Lippershey erfundenen Fernrohrs – ein einfaches Fernrohr mit zunächst 4-facher und später bis zu 33-facher Vergrößerung und beobachtete den Himmel:
Er baute mit Hilfe seiner erlernten Schleifkunst aus Brillenlinsen – nach dem Vorbild des in Holland von Jan Lippershey erfundenen Fernrohrs – ein einfaches Fernrohr mit zunächst 4-facher und später bis zu 33-facher Vergrößerung und beobachtete den Himmel:
- er entdeckte die vier Monde des Jupiter (Io, Europa, Ganymed und Kallisto)
- er erkannte die Phasengestalt der Venus (Sichel und Dichotomie)
- er beschrieb die Ringe des Saturn
- er beobachtete die Schatten der Mondgebirge
- er sah die Sonnenflecken und damit die Rotation der Sonne
- er nahm wahr, dass die Milchstraße nicht ein nebliges Gebilde ist, sondern aus einzelnen Sternen besteht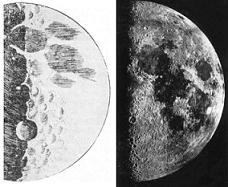 - er bemerkte, dass der Mond nicht leuchtet, sondern von der Sonne angeleuchtet wird
- er bemerkte, dass der Mond nicht leuchtet, sondern von der Sonne angeleuchtet wird
- er stellte fest, dass die Planeten - im Gegensatz zu den Fixsternen - als Scheiben zu sehen sind
All diese Beobachtungen und eine Federzeichnung der Mondoberfläche veröffentlichte er im Sidereus Nuncius, der Galilei berühmt machte.
Außerdem bestätigten sie ihn in seiner ohnehin schon für ihn feststehenden Überzeugung von der Richtigkeit des kopernikanischen Weltbildes.
- Entwicklung eines Thermometers (noch sehr ungenau arbeitend)
- Erfindung der hydrostatischen Waage:
1586 konstruierte Galilei – angeregt durch die Arbeiten von Archimedes – eine hydrostatische Waage, mit der man spezifische Gewichte bestimmen konnte und löste damit ein antikes Problem.
- Erfindung einer Rechenmaschine:
Mit dieser Rechenmaschine kann man aus der Stellung der Jupitermonde den geographischen Standpunkt bestimmen.
- Entdeckung der Libration des Mondes:
Kurz vor seiner Erblindung stellte er die schwankende Bewegung des Mondes (Libration) fest. Diese Libration setzt sich aus folgenden vier Anteilen zusammen: Libration in der Länge durch die Ellipsenbahn; Libration in der Breite durch die Neigung der Rotationsachse; parallaktische Libration durch den Blickwinkel und schließlich die physische Libration durch die Mondform (der Mond ist keine ideale Kugel).
- Einige nützliche Erfindungen:
Man fand Skizzen von Geräten wie einer Kombination aus Kerze und Spiegel, um damit das Licht durchs ganze Haus leiten zu können; einem automatischen Tomatenpflücker; einem Taschenkamm, der auch als Besteck verwendet werden konnte oder einer Art Vorläufer des Kugelschreibers.
- Erkenntnisse bezüglich des Weltbildes:
Galilei war von folgenden Tatsachen überzeugt:
- die Sonne steht im Mittelpunkt des Planetensystems
- die Erde ist ein Planet wie Merkur , Venus und Mars
- alle Körper auf Erden und im Weltall bewegen sich nach festen Gesetzen
Galileis wichtige Werke:
- Sidereus nuncius, 1610
deutsch: Nachricht von neuen Sternen - Saggiatore 1623
deutsch: Prüfer mit der Goldwaage - Dialogo sopra i due massimi sistemiFlorenz 1632
deutsch: Dialog über die beiden hauptsächlichen Weltsysteme - Discorsi e dimostrazioni matematicheLeiden 1638
deutsch: Unterredung und mathematische Demonstration über zwei neue Wissenszweige die Mechanik und die Fallgesetze betreffend

Galilei zu Ehren wurden folgende Dinge nach ihm benannt:
- im cgs-System die Einheit für die Erdbeschleunigung „Gal“
- ein Krater auf dem Mond
- das Galileo-Thermometer
- die Raumsonde Galileo, gebaut zur Erforschung des Planeten Jupiter
- das zukünftige Satellitennavigationssystem Galileo
- eine dimensionslose Kennzahl der Strömungsmechanik (Galilei-Zahl)
- die vier größten Monde des Jupiter (die Galileischen Monde)
I. Einleitung
Wie kam es zur Fassregel?
Auf die Idee, sich mit der Berechnung von Flächeninhalten unter einer Fasskurve und dem entsprechenden Fassvolumen zu befassen, kam Johannes Kepler, als er einige Fässer Wein, die er für seine zweite Hochzeit brauchte, bezahlen musste. Er erkannte dabei, dass der Preis, welcher sich nach dem Volumen des Fasses richtete, auf Grund von Ungenauigkeiten beim Errechnen des Volumens des gefüllten Fasses nicht exakt war. Bis dahin war es üblich, das Volumen von Fässern mit der Visiermethode zu bestimmen. Diese ließ jedoch außer Acht, dass nicht jedes Fass mit denselben Proportionen gebaut wurde. Demnach kann ein sehr hohes Fass mit schmalen Böden denselben Rauminhalt wie ein niedrigeres Fass mit breiteren Böden haben. Außerdem beauftragte der Magistrat der Stadt Ulm Kepler 1615, neue Maßeinheiten für die Stadt festzulegen.
Zitat von Kepler:
"Als einige Fässer eingekellert waren, kam am 4.Tag der Verkäufer mit der Messrute, mit der er alle Fässer, ohne Rücksicht auf ihre Form, ohne jede weitere Überlegung oder Rechnung ihrem Inhalte nach bestimmte. Die Visierrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden geführt, und als die beiden Längen gleich gefunden worden waren, ergab die Marke am Spundloch die Zahl der Eimer im Fasse. Ich wunderte mich, dass die Querlinie durch die Fasshälfte ein Maß für den Inhalt abgeben könne, und bezweifelte die Richtigkeit der Methode, denn ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Inhalt könnte dieselbe Visierlänge besitzen.
Es schien mir als Neuvermähltem nicht unzweckmäßig, ein neues Prinzip mathematischer Arbeiten, nämlich die Genauigkeit dieser bequemen und allgemein wichtigen Bestimmung nach geometrischen Grundsätzen zu erforschen und die etwa vorhandenen Gesetze ans Licht zu bringen."
Wozu dient die Keplersche Fassregel?
Mit Hilfe der Keplerschen Fassregel ist es näherungsweise möglich ohne Integralrechnung die Fläche unter einer Kurve zu bestimmen.
Die Keplersche Fassregel basiert auf recht einfachen Größen: der Höhe h des Fasses, dem Radius des Deckels, dem Radius des Bodens und dem Radius auf halber Höhe des Fasses.
Den Deckelradius nennen wir f(r), den Mittelradius f(m) und den Bodenradius f(s) (Die komisch anmutenden Benennungen resultieren aus der Herleitung der Keplerschen Fassregel, die später noch genauer aufgezeigt wird). Dann ergibt sich nach Kepler die relativ einfache Regel zur Bestimmung der Querschnittsfläche A eines Fasses, die sogenannte "Keplersche Fassregel".
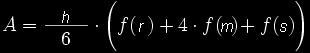
Außerdem erhält man näherungsweise, aber relative genau, das Volumen eines Fasses:
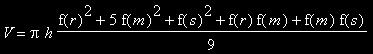
II. Herleitung
Wie kann man der Keplerschen Fassregel mathematischen Halt verleihen?
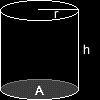 Nun, stellen wir uns zunächst vor, das Fass wäre eine einfache Tonne, hätte also einen geraden anstatt eines gewölbten seitlichen Randes. Dann wäre das Volumen dieses Körpers einfacher zu berechnen, nämlich als das Produkt aus der kreisförmigen Grundfläche A und der Höhe h.
Nun, stellen wir uns zunächst vor, das Fass wäre eine einfache Tonne, hätte also einen geraden anstatt eines gewölbten seitlichen Randes. Dann wäre das Volumen dieses Körpers einfacher zu berechnen, nämlich als das Produkt aus der kreisförmigen Grundfläche A und der Höhe h.
Die Grundfläche wiederum ergibt sich aus dem Produkt des Quadrats des Radius r mit der Kreiszahl Pi: 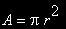
Das Volumen V wäre demnach: 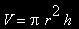
Wie aber berechnet sich das Volumen eines Fasses, das ja einen Bauch und keinen geraden Rand hat?
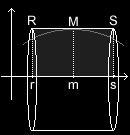
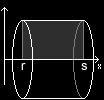 Wir bedienen uns eines einfachen, in der Mathematik oft angewandten Tricks: Wir reduzieren das Problem zunächst auf ein einfacheres, eines welches wir schon ohne große Mühe lösen können, nämlich auf die oben erwähnte Tonne; allerdings betrachten wir unsere Tonne nun auf eine andere Weise: wir stellen sie nicht mehr auf, sondern wir legen sie auf die Seite, oder noch besser: wir hängen sie entlang ihrer Mitte auf, so dass die Seiten nun parallel zum Boden liegen. Zum Aufhängen benutzen wir keine Schnur, sondern die x-Achse eines Koordinatensystems zwischen den Stellen r (Mitte des Fassdeckels) und s (Mitte des Fassbodens). Den Anfangs- und den Endpunkt des Bogens nennen wir entsprechend R bzw. S.
Wir bedienen uns eines einfachen, in der Mathematik oft angewandten Tricks: Wir reduzieren das Problem zunächst auf ein einfacheres, eines welches wir schon ohne große Mühe lösen können, nämlich auf die oben erwähnte Tonne; allerdings betrachten wir unsere Tonne nun auf eine andere Weise: wir stellen sie nicht mehr auf, sondern wir legen sie auf die Seite, oder noch besser: wir hängen sie entlang ihrer Mitte auf, so dass die Seiten nun parallel zum Boden liegen. Zum Aufhängen benutzen wir keine Schnur, sondern die x-Achse eines Koordinatensystems zwischen den Stellen r (Mitte des Fassdeckels) und s (Mitte des Fassbodens). Den Anfangs- und den Endpunkt des Bogens nennen wir entsprechend R bzw. S.
Den Radius r der Tonne drücken wir über eine Funktion f aus, dann errechnet sich das Volumen nun als 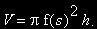
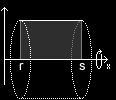 Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor, sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt. So merken wir schnell, dass es die Fläche des Rechteckes ist, die das Volumen des Rotationskörpers", also in unserem Falle des Fasses, bestimmt. Die sogenannte Keplersche Fassregel" gibt uns den Inhalt solcher Flächen an.
Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor, sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt. So merken wir schnell, dass es die Fläche des Rechteckes ist, die das Volumen des Rotationskörpers", also in unserem Falle des Fasses, bestimmt. Die sogenannte Keplersche Fassregel" gibt uns den Inhalt solcher Flächen an.
Wie ersetzen wir unsere Tonne nun wieder durch das Fass?
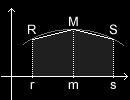 Gerade dabei ergibt sich allerdings ein Problem: Mit einer geeigneten Funktion f können wir zwar leicht den gewölbten Rand des Fasses nachzeichnen, um so zu einer geeigneten Rotationsfläche zu gelangen. f(x) gibt uns den Radius des Fasses aber nur an einer einzigen Stelle (nämlich an der Stelle x) an. Daher unterteilen wir den Bogen, den die Funktion f nachzeichnet, in zwei Abschnitte. Idealerweise wählen wir die halbe Höhe des Fasses als Trennstelle, die Stelle nennen wir m, den entsprechenden Punkt auf dem Bogen (bzw. dem Fassrand) nennen wir M. Dann verbinden wir die Punkte R und M sowie M und S jeweils durch Strecken, um den Bogen grob schematisiert nachzeichnen zu können.
Gerade dabei ergibt sich allerdings ein Problem: Mit einer geeigneten Funktion f können wir zwar leicht den gewölbten Rand des Fasses nachzeichnen, um so zu einer geeigneten Rotationsfläche zu gelangen. f(x) gibt uns den Radius des Fasses aber nur an einer einzigen Stelle (nämlich an der Stelle x) an. Daher unterteilen wir den Bogen, den die Funktion f nachzeichnet, in zwei Abschnitte. Idealerweise wählen wir die halbe Höhe des Fasses als Trennstelle, die Stelle nennen wir m, den entsprechenden Punkt auf dem Bogen (bzw. dem Fassrand) nennen wir M. Dann verbinden wir die Punkte R und M sowie M und S jeweils durch Strecken, um den Bogen grob schematisiert nachzeichnen zu können.
Zwar verlieren wir durch die "Schematisierung" (man sagt in der Mathematik: "Approximation" oder "Annäherung an die Kurve") an Genauigkeit, dafür können wir die erhaltene Rotationsfläche des manipulierten Fasses leicht errechnen: Beide Abschnitte stellen je ein Trapez dar, dessen Flächeninhalt A gleich dem Produkt aus der Länge der Grundseite, also in unserem Fall der halben Höhe h des (stehenden) Fasses, und der mittleren Höhe des Trapezes. 
Analog erhalten wir für den zweiten Abschnitt den Flächeninhalt: 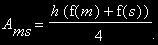
Beide zusammen ergeben die Rotationsfläche der gesamten Figur: 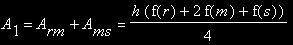
Bei der Schematisierung ist die Rotationsfläche und damit auch unser Fass etwas zu klein geraten, da die Strecken RM und MS unterhalb des Bogens verlaufen.
Können wir diesen Fehler wieder etwas ausgleichen?
Als Ausgleich zu dem Verlust an Rotationsfläche, der bei der Schematisierung entstanden ist, gibt es ein weiteres Verfahren, mit dem man die Fläche unterhalb des Bogens ebenfalls schematisiert darstellt; hierbei wird die Fläche aber vergrößert, was als Ausgleich zum Verlust beim ersten Verfahren dienen soll: 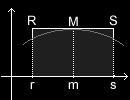 Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m) zwischen den Stellen a und b, das also genau so lang ist wie das (stehende) Fass hoch; der Flächeninhalt dieses Rechtecks ist demnach:
Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m) zwischen den Stellen a und b, das also genau so lang ist wie das (stehende) Fass hoch; der Flächeninhalt dieses Rechtecks ist demnach: 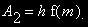
Es bleibt die Frage, wie wir beide Verfahren miteinander kombinieren sollen.
Nun, da das erste Verfahren um den Faktor 2 genauer ist, denn hier haben wir das Fass zur Schematisierung in zwei Abschnitte unterteilt, verrechnen wir es einfach mit dem zweiten, bei dem wir das gesamte Fass sozusagen in einem Abschnitt schematisiert haben, in der Wertigkeit 2 zu 1: 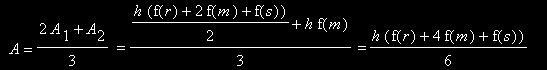
Bei der erhaltenen Näherungsformel handelt es sich um die "Keplersche Fassregel".
Um aber das Volumen eines Fasses zu berechnen, müssen wir noch weiter überlegen, denn diese Keplersche Fassregel gibt uns ja offensichtlich nur die halbe Querschnittsfläche eines Fasses an, nicht aber dessen Volumen.
Wie berechnet man also das Volumen nach Kepler?
Nun, wir vollziehen wieder jeden Schritt beider Näherungen nach: 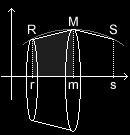 Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines Kegelstumpfes erhält man aus, wobei R und r die Radien, h die Höhe des Kegelstumpfes sind :
Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines Kegelstumpfes erhält man aus, wobei R und r die Radien, h die Höhe des Kegelstumpfes sind : 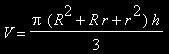
Bei unseren beiden Trapezen wären das also 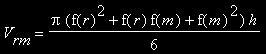
und 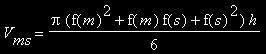
Beide zusammen ergeben wieder unsere erste Näherung: 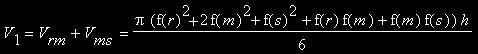
 Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als
Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als 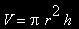 , wobei r der Radius und h die Höhe ist. In unserem Beispiel wäre f(m) der Radius, das Volumen der zweiten Näherung folglich :
, wobei r der Radius und h die Höhe ist. In unserem Beispiel wäre f(m) der Radius, das Volumen der zweiten Näherung folglich : 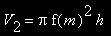
Verrechnen wir wieder beide Näherungen in der Wertung 2:1 miteinander, so erhalten wir als endgültige Näherung für das Volumen :
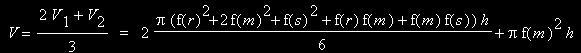
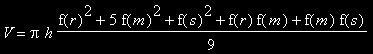
Für den Spezialfall f(r) = f(s) ergibt sich dann:
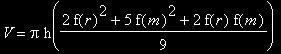
III. Mängel der Regel / Visiermethode
Mängel der Keplerschen Fassregel
Je nach Faßform ist die Keplersche Faßregel mehr oder weniger ungenau, da es sich nur um eine Näherungsformel handelt. Aber verglichen mit der geringeren Genauigkeit der Visiermethode und dem größeren mathematischen Aufwand der Integralrechnung dürfte die Keplersche Fassregel wohl die praktischste aller Lösungen sein. Zur Berechnung benötigt man nur vier Größen; diese sind dazu noch recht leicht zu ermitteln: den Radius des Deckels, den des Bodens und den des Faßbauches auf halber Höhe, schließlich noch die Höhe des Fasses. Und für diesen geringen Aufwand beweist die Keplersche Faßregel eine erstaunliche Genauigkeit, die Abweichung liegt, zumindest bei faßähnlichen Gebilden, meistens im Promille-Bereich. Dieser Fehler ist jedenfalls kleiner als die durch genaues oder ungenaues Füllen des Fasses entstehenden Unterschiede!
Mängel der Visiermethode
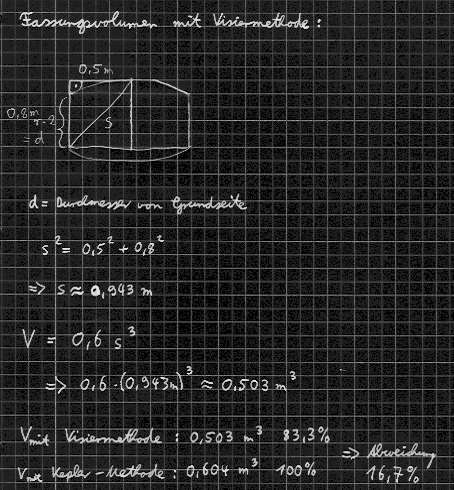
Bedenkt man nur die zu messenden Größen, so erscheint die Visiermethode mit nur einer solcher Größe, nämlich den Abstand vom Spundloch in die tiefste Bodenecke, sehr leicht anwendbar. Zwar ist die erzielte Genauigkeit recht groß, wenn man die Einfachheit der Methode bedenkt, aber dennoch - insbesondere im Vergleich mit den anderen hier vorgestellten Methoden - nicht zufriedenstellend.
Der Hauptmangel der Visiermethode ist in der Herleitung deutlich zu erkennen: Man geht von einer bestimmten Fassform aus, bei der die Oberseite und die Unterseite gleich lang, die Verlängerung der Oberseite bis über am weitesten ausgewölbten Punkt des Fassbauches genauso lang ist wie die halbe Höhe des Fasses.
Darüber hinaus wird, ebenfalls in der Herleitung erkennbar, aufgerundet: 0,5555...s³ wird gerundet zu 6s³.
Ob sich diese beiden Rundungen gegenseitig aufheben oder eher verschlimmern, hängt von der endgültigen Form des einzelnen Fasses ab. Wie sehr sich diese Rundungen bemerkbar machen, zeigt der Genauigkeitsvergleich der einzelnen Methoden.
Herleitung der Visisermethode:
Ersetzt man das Fass durch einen Zylinder, dessen Durchmesser halb so groß wie seine Höhe ist so gilt für sein Volumen folgendes:
allgemein: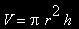
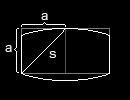
für diesen Fall: 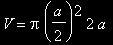
(wobei "(a/2)" den halben Durchmesser und somit den Radius der Grundseite darstellt).
Und da s² = 2a² (nach Pythagoras), folgt:
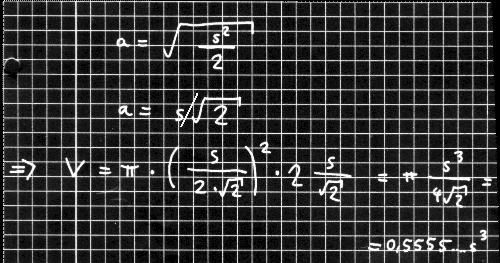
Man kann also ungefähr sagen V = 0,6 s³
Dieser letzte Term entspricht genau der Visiermethode.
Wie man hier sieht, ist neben der Abweichung der Formen noch eine Ungenauigkeit beim Aufrunden vorhanden, daher ist die Visiermethode gerade in puncto Genauigkeit mit erheblichen Mängeln versehen.
IV. Anwendungsmöglichkeiten
Mit Hilfe der Keplerschen Fassregel kann man mit relativ wenig Aufwand eine krummlinig begrenzte Fläche A im Intervall [a,b] ermitteln.
Dazu ersetzt man den Funktionsgraphen durch eine Parabel 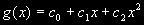 , die den Funktionsgraphen f(x) in den drei Punkten P0, P1, P2 schneidet.
, die den Funktionsgraphen f(x) in den drei Punkten P0, P1, P2 schneidet. 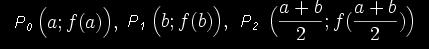
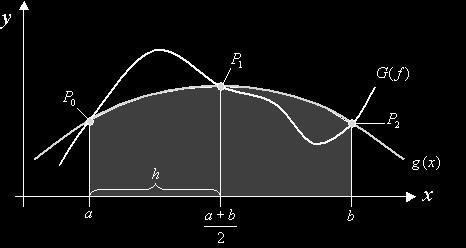
Die drei Funktionswerte erhält man, indem man a, [(a+b)/2) und b in die Parabelgleichung einsetzt.
Jetzt muss man diese nur noch in die Formel zur Keplerschen Fassregel einsetzen.
Weitere Anwendungsmöglichkeiten u.a.:
Berechnung von...
...Kreisflächen
...Fläche unter der Sinuskurve
...Fläche unter der Parabel
...Kegeln (-stumpfe)
...Kugeln
...Rotationsparaboloiden ( = Rotationskörper einer Parabel )
V. Beispiel-Aufgabe
Verfolgt man die Entwicklung der Rotationskörper historisch, so kommt man nicht umhin zu erkennen, dass am Anfang eine recht pragmatische Frage stand. Die Frage war: „Wie kann man das Volumen eines Weinfasses berechnen“.
Deshalb soll auch die hier vorgestellte Beispiel-aufgabe auf genau diese Ursprungsfragestellung zurückgehen:
Die Innenwand unseres Fasses wird durch die Funktion f(x)= -(2/5)x^2+0,5.
Es hat eine Höhe von einem Meter und der Radius des Deckels und des Bodens stimmen überein.
Die Außenwand wird durch die Funktion f(x)= -(2/5)x^2+0,55 festgelegt (1LE entspricht 1m).
a) Bestimme die notwendigen Radien und überprüfe durch Berechnung des entsprechenden Rotationskörpers, ob mit der Fassregel das Volumen unseres Fasses näherungsweise berechnet werden kann.
b) Bestimme die Masse des leeren Holzfasses unter der Annahme, dass das verwandte Holz eine Dichte von 1070 (kg/m^3) hat.
Teilaufgabe a): Teilaufgabe b):
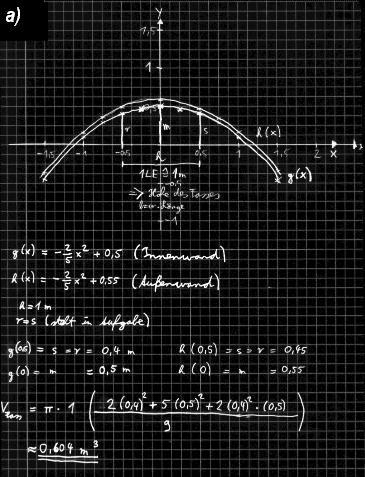
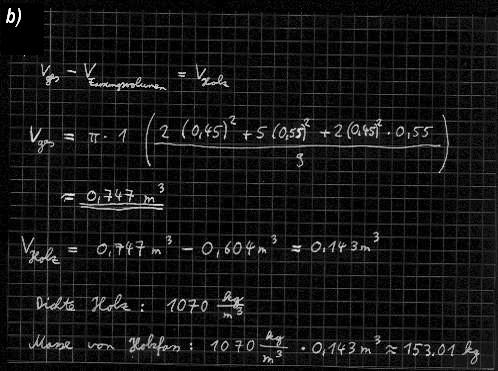
Ein Vergleich des errechneten Volumens mit dem Ergebnis das die Visiermethode ergibt:
I. Kepler und die Philosophie
Am 15. Mai 1618 veröffentlichte Kepler sein Werk „Harmonices Mundi“, das vom Lateinischen ins Deutsche übersetzt die „Harmonie der Welt“ bedeutet. In diesem Buch entwickelte Kepler den Begriff „Sphärenharmonie“, der auf Pythagoras zurückgeht, weiter.
Kepler war nicht nur Naturwissenschaftler sondern auch Philosoph. Kepler hatte drei Grundgedanken:
- Das All gehorche einer einheitlichen Gesetzmäßigkeit.
- "Der menschliche Geist durchschaue quantitative Verhältnisse am klarsten; er sei recht eigentlich geschaffen, diese aufzufassen."
- "Ubi materia, ibi geometria.” (Wo Materie ist - da ist Mathematik)

Kepler suchte ähnlich wie Pythagoras das Geheimnis der Welt nicht wie die Milesier in einem Urstoff, sondern in einem Urgesetz. So waren für Pythagoras die Zahlen das eigentliche Geheimnis und die grundlegenden Bausteine der Welt.
In der europäischen Neuzeit haben viele Philosophen, wie auch z.B. Nikolaus von Kues, die Meinung vertreten, dass „Gott die Welt unter Zugrundelegung mathematischer Gesetze geschaffen hat“.
Kepler sah den Fehler der antiken griechischen Philosophen darin, dass sie versuchten, die Natur mit qualitativ verschiedenen Kräften zu erklären. Im Gegensatz dazu sah er die Natur als durch und durch einheitlich und die Unterschiede in ihr nur als quantitative.
II. Qualität und Quantität
Was versteht man unter Qualität?
Das Wort kommt aus dem Lateinischen und ist mit Wörtern wie Beschaffenheit, Eigenschaft, Wert etc. zu übersetzen. In der Philosophie bedeutet dieser Begriff darüber hinaus "etwas Neues", oft "Höheres", auf das Vorherige beruhend aber dennoch anderes.
Die Philosophen konzentrieren sich auf die Qualitäten im Sein und auf die Entstehung neuer Werte im Verlauf der Entwicklung bzw. der Zeit.
Beispiele hierfür wären zum Beispiel die Entstehung von:
- Geist
(der Gebrauch dieses Wortes ist nicht einheitlich, häufige Verwendungen im Sinne von „aktivem Bewusstsein“, Vernunft, Verstand, Seele) - Gesellschaft
(= sowohl die Menschheit als Ganzes als auch bestimmte Gruppen von Menschen, beispielsweise ein Volk, oder ein strukturierter, räumlich abgegrenzter Zusammenhang zwischen Menschen) - Ethik
((von ethos) = die Lehre vom richtigen Handeln und Wollen, eng damit verbunden ist die Frage, was gut und böse ist) - Ästhetik
(= ursprünglich Lehre von den sinnlichen Wahrnehmungen, heute versteht man darunter in erster Linie die Lehre von den Gesetzmäßigkeiten und der Harmonie in Natur und Kunst)
Was versteht man unter Quantität?
Das Wort Quantität stammt aus dem Lateinischen und entspricht der mess- oder zählbaren Menge.
Diese Rückführung qualitativer Unterschiede auf quantitative Verhältnisse war eine der Voraussetzungen für den Erfolg der modernen Naturwissenschaften.
III. Das anthropische Prinzip
Keplers Anschauungen entsprachen dem, was man heute als anthropisches Prinzip bezeichnet:
„Ich fühle mich von einer unaussprechlichen Verzückung ergriffen ob des göttlichen Schauspiels der himmlischen Harmonie. Denn wir sehen hier, wie Gott gleich einem menschlichen Baumeister, der Ordnung und Regel gemäß, an die Grundlegung der Welt herangetreten ist.“
 Das anthropische Prinzip (von griechisch anthropos „Mensch“) besagt, dass die enorme Vielzahl von Naturgesetzen und Naturkonstanten im Universum exakt so aufeinander abgestimmt sind, dass sie Leben ermöglichen, welches diese unwahrscheinlichen Bedingungen als solche auch zu erkennen vermag.
Das anthropische Prinzip (von griechisch anthropos „Mensch“) besagt, dass die enorme Vielzahl von Naturgesetzen und Naturkonstanten im Universum exakt so aufeinander abgestimmt sind, dass sie Leben ermöglichen, welches diese unwahrscheinlichen Bedingungen als solche auch zu erkennen vermag.
Die Entwicklung von irdischen Leben wäre wohl unmöglich, wenn
- die physikalischen Gesetze
- die Werte der Naturkonstanten
merklich von den im Labor festgestellten abweichen würden.
Daher dürften wir auch nicht imstande sein, ein wesentlich anderes Universum zu beobachten als das unsrige.
Daraus folgt:
- Sie kann der menschliche Geist in mehr oder weniger weiten Grenzen konzipieren und begreifen
- Sie haben mathematische Form
Nicht nur dass der Mensch in das Universum hineinpasst, das Universum passt auch zum Menschen. Man stelle sich ein Universum vor in dem sich irgendeine der grundlegenden dimensionslosen physikalischen Konstanten in die eine oder andere Richtung um wenige Prozent verändern würde. In einem solchen Universum hätte der Mensch nie ins Dasein kommen können. Das ist der Dreh- und Angelpunkt des anthropischen Prinzips. Gemäß diesem Prinzip liegt dem gesamten Mechanismus und dem Aufbau der Welt ein die Existenz von Leben ermöglichender Faktor zugrunde.
(John Barrow und Frank Tipler The Anthropic Cosmological Principle Seite 7)
Mit folgendem Satz führte Brandon Carter 1973 das Anthropische Prinzip in die wissenschaftliche Diskussion ein:
"We must be prepared to take account of the fact that our location in the universe is necessarily privileged to the extent of being compatible with our existence as observers."
"Cogito ergo mundus talis est"
= Ich meine, also ist das Weltall so beschaffen (daß es mich als denkendes Wesen geben kann)
Die Vertreter des AP weisen darauf hin, dass das Universum in seiner Gesamtheit, (von wem oder was auch immer) so fein abgestimmt ist, dass sich daraus zwangsläufig Leben in der Form wie wir es kennen entwickeln musste. Denn wiche auch nur eine der grundlegenden naturwissenschaftlichen Konstanten von ihrem Wert ab, so wäre das Leben in seiner Form nicht möglich. Dass sich binnen 13,7 Milliarden Jahren (seit dem „Urknall“) quasi aus dem Nichts Bewusstsein bilden konnte, setzte schier unzählige Anfangsbedingungen, Prozesse und Evolutionen voraus, von denen uns allenfalls nur Mosaiksteine bekannt sind. So hängt die Entwicklung des Kosmos entscheidend von den Anfangsbedingungen der Expansion und den Naturkonstanten Lichtgeschwindigkeit c oder dem Planckschen Wirkungsquantum h und den Massen der Elementarteilchen sowie der Kräftehierarchie der Wechselwirkungen ab.
Beim Studium des APs muss man sich mit den beiden hauptsächlichen Varianten auseinandersetzen:
- Schwaches Anthropisches Prinzip (engl. weak anthropic principle, WAP):
„Die beobachteten Werte aller physikalischen und kosmologischen Größen sind nicht gleich wahrscheinlich aber sie nehmen Werte an, die beschränkt sind durch die Erfordernisse für die Existenz von Orten an denen Kohlenstoff basiertes Leben entwickeln kann und durch die Erfordernis dass das Universum bereits alt genug sein muss, dass dieser Vorgang bereits eingetreten ist.“ - Starkes Antropisches Prinzip (engl. strong anthropic principle, SAP):
„.. das Universum (und deswegen die fundamentalen Parameter von welchen es abhängt) muss derart sein, dass es die Entstehung von Beobachtern in ihm in manchen Phasen erlaubt.“
Die schwache Version wurde als „Argument aus Mangel an Vorstellungskraft“ kritisiert für die Annahme, dass keine anderen Formen von Leben möglich seien. Auch die starke Version wurde kritisiert als nicht wissenschaftlich prüfbar bzw. nicht falsifizierbar sowie als schlicht unnötig. Das Wort „muss“ in der Definition des starken APs ist für die mehrdeutige Interpretation des Prinzips verantwortlich, denn es kann als Forderung der schlichten logischen Verträglichkeit der Beobachtungsdaten mit der Beobachterexistenz als auch in einem tieferen teleologischen Sinn gedeutet werden. Weil das starke AP teleologisch gedeutet werden kann, wird ihm häufig ein unwissenschaftlicher Charakter unterstellt.
Es gab noch viele andere Wissenschaftlicher, die sich zu dem AP äußerten, so zum Beispiel:
- Barrow und Tipler: „Intelligente Informationsverarbeitung muss im Universum entstehen, und, wenn sie einmal entstanden ist, wird sie niemals aussterben“
Sie nannten es das endgültige anthropische Prinzip (Final Anthropic Principle).
- John Wheeler: „Beobachter sind notwendig, um das Universum zu erzeugen.“
IV. Was ist „Teleologie“?
Die Teleologie (griechisch, im altgriechischen Sinn Ziel, Sinn und Lehre) ist die Lehre der ziel- und zweckbestimmten Ordnung von Gegenständen und Ereignissen.
Nach teleologischen Anschauungen, sind Naturphänomene einer inneren Zweckgerichtetheit unterstellt. Dabei wird nach Aristoteles zwischen der causa materialis (=Stoffursache) und der causa finalis (=Zweckursache) unterschieden. Man versucht Vorgänge in der Natur nicht über Wirkursachen sondern über Zielzustände zu erklären. So sagt die Teleologie aus, dass es in der Natur so etwas wie Absicht und Planung gebe.
Das teleologische Prinzip wird mittlerweile von vielen Wissenschaften abgelehnt. Man hat zum Beispiel in der Biologie versucht die gesamte Entwicklung eines Eies zu einer bestimmten Spezies teleologisch zu erklären. Jedoch konnte keine Erklärung für das Wirken eines solchen letzten Prinzips gefunden werden und die Erkenntnisse der Genetik und der Paläontologie (= Wissenschaft von den Lebewesen vergangener Erdzeitalter) brachten die Teleologie schließlich vollständig in Verruf. Manche Philosophen sehen es als größte Leistung Darwins an, dass er Aristoteles' vierte und letzte Ursache widerlegt hätte, indem er zeigte, dass eine Entwicklung hin zu einem bestimmten Ziel durch die natürliche Auslese erklärt werden könne.
I. Allgemeines

In diesem Buch, das übersetzt Weltharmonik heißt, legte Kepler in ausgereifter Form 1619 seine Gedanken über den Aufbau der Welt dar.
Kepler fasst es geradezu als Pflicht auf, „in behutsamer Weise nach den Zahlen, Maßen und Gewichten zu forschen, nach deren Norm Gott alles geschaffen hat“, also nach deren „Harmonien“. Er bewegt sich dabei auf drei Gebieten, der Geometrie, Astronomie und Musik, das ist der Teil, der hier genauer in Augenschein genommen werden soll.
II. Wie kam er auf die Musik?
Seine Überlegungen waren eine Anknüpfung an die griechische Harmonielehre des Pythagoras, die die Verhältnisse der Tonabstände zueinander beschreibt und gerade durch die Saiteninstrumente an Bedeutung gewinnt.
Teilt man sie 2/3 erhält man die Quinte. Die weltenbildenden Verhältnisse sind 1/2, 3/5, 5/8, 2/3, 3/4, 4/5, 5/6.
Jetzt beginnt Kepler mit seinen Rechnungen. Er begründet jeden Schritt den er tut entweder mit mathematischen Gesetzen oder auf seiner Logik basierenden Aussagen. Das Verhältnis 1/2 beschreibt er zum Beispiel so:
„Ist nicht die Kreisteilung 1/2 die einfachste und ursprünglichste, wie auch das musikalische Intervall 1/2 die am meisten auffallende und ursprüngliche Oktav bildet?"
Er spekuliert weiter: „So hat Gott nicht einmal die Töne ohne Geometrie in die Welt eingeführt."
„Diese Seele wird froh gestimmt, wenn sie harmonische Töne, übelgelaunt, wenn sie nichtharmonische Töne wahrnimmt. Von diesen seelischen Stimmungen rührt die Bezeichnung Konsonanzen für die harmonischen und die Bezeichnung Dissonanzen für die nichtharmonischen Proportionen her. Kommt dazu noch die weitere harmonische Proportion, die der zeitlichen Länge und Kürze der Töne und Stimmen, dann regt die Seele ihren Körper zu Tanzbewegungen, die Zunge zu beschwingter Rede nach den gleichen Gesetzen an… Alles lebt, solange die Harmonien dauern, alles erschlafft, wenn sie gestört sind.“
Auf dieser Grundlage baut Kepler seine Harmonielehre auf, indem er sie an einer Seite eines Monochords (eine gespannte Saite mit Resonanzkörper) untersucht. Er erkennt die Teilungen die Wohlklänge liefern. Und nach entsprechender Auswahl gelangt er zu 7 Intervallen („Die Zahl der harmonischen Teilungen einer Saite ist 7 und nicht größer.“), die auch die musikalischen Urharmonien darstellen, sie lassen sich alle auf urbildliche geometrische Formen zurückführen. Er entwickelt einen Harmonienstammbaum.

Diese Intervalle: Oktav, Quint, Quart, große Terz, Kleine Terz, große Sext und kleine Sext beruhen alle auf sehr einfachen Zahlenverhältnissen, nämlich auf Schwingungsverhältnissen von 1:2, 2:3, 3:4, 4:5, 5:6, 5:8 und 3:5.
„Ein dissonantes Intervall wie der Tritonus (=übermäßige Quart) entspricht dem nicht so einfachen Verhältnis von 45:64.“
Als einen anderen Weg, um zu den Urharmonien zu gelangen, entwickelt Kepler eine aus sich selbst hervorgehende Ahnenreihe der harmonischen Teilung einer Saite, wie der harmonische Stammbaum zeigt.
Die Zahlenverhältnisse (Brüche) 1/1, 1/2, 1/3, 2/3 usw. des Stammbaums geben an, wie eine Saite geteilt werden muss. 1/3 bedeutet dabei z.B., dass eine Saite in 1+3 = 4 gleiche Teile unterteilt wird. Es ergeben sich daraus 3 Schwingungsverhältnisse, nämlich das der Teile untereinander: 1 zu 3 (=1/3) und die Verhältnisse der Teile zum Ganzen: 1/4 und 3/4. Mit den entstehenden Verhältnissen 1/4 und 3/4 werden neue Teilungen der Saite möglich, die nach dem gleichen Prinzip weitergeführt werden bis eine 7er, 9er, 11er und 13er Teilung der Saite gefordert wird, die zum Abbruch der Reihe führt, da diese aufgrund Keplers Untersuchungen dissonant sind, weil ein 7-Eck, 9-Eck, 11-Eck und 13-Eck im Kreis nicht mit Zirkel und Lineal konstruierbar ist.

Prinzip der Entwicklung der Ableitung der sieben konsonanten Intervalle
Daraus ergeben sich innerhalb einer Oktav sieben konsonante Intervalle:
- 1/2 Oktav
- 2/3 Quint
- 3/4 Quart
- 3/5 große Sext
- 4/5 große Terz
- 5/6 kleine Terz
- 5/8 kleine Sext
„Ich habe diese 7 Schnitte der Saite zuerst aus dem Gehör gefunden, also in einer Zahl, die gleich ist der Zahl der Harmonien innerhalb einer Oktav. Hernach habe ich die Ursachen nicht ohne große Mühe aus den tiefsten Gründen der Geometrie ermittelt.“
Dissonanzen in der Musik sind jedoch für Kepler nichts Schlechtes, sondern nur weniger zusammenklingende Proportionen:
„Was die erste und hauptsächlichste Würze des melodischen Gesangs anlangt, die Dissonanz, so darf diese nicht irgendeinem beliebigen unharmonischen Intervall entnommen werden, sondern nur den harmonischen Intervallen.
Wenn ferner auch hervorragende Meister bisweilen von größeren Dissonanzen Gebrauch machen, so dass der dissonierende Ton um einen ganzen Ton sich von dem unterscheidet, der eine Konsonanz bilden würde, so geschieht das nur, um die mächtigsten Gemütsbewegungen auszudrücken oder hervorzurufen. Die gewöhnliche, mit Wohlgefallen verknüpfte und daher in gewisser Weise natürliche Dissonanz wird von dem Halbton gebildet. Die Ursache hiefür ist (damit das Ende dem Anfang entspricht) in den tiefsten Gründen der Geometrie zu suchen“
Fazit:
Nicht die Zahlen allein, sondern das menschliche Gehör legt die Grenze zwischen Dissonanz und Konsonanz fest. Aber: Konsonanzen haben sich in der Geometrie als das Verhältnis von konstruierbaren Kreisteilen zum ganzen Kreis erwiesen.
III. Doch wie stellt Kepler den Bezug von der Astronomie zur Musik her?
„Nicht darauf muss man sehen, so dachte ich, wie weit jeder einzelnen Planet von der Sonne entfernt ist, noch darauf, welche Strecke er an einem Tag durchmisst. Denn dies ist Gegenstand wissenschaftlicher, astronomischer Erkenntnis, nicht Sache des Instinkts. Man muss vielleicht die Größe des Winkels ins Auge fassen, den die tägliche Bewegung eines jeden Planeten am Sonnenkörper ausmacht, oder die Größe des Bogens, den er an einem Tag auf einem gemeinsamen, um die Sonne beschriebenen Kreis, d.h. auf der Ekliptik, zurückzulegen scheint. Es können dann diese scheinbaren Größen durch die Vermittlung des Lichts auf den Sonnenkörper übertragen werden…“
So wie der Sehvorgang des Auges wesentlich durch den Einfallswinkel des Lichtstrahles beeinflusst würde, so nimmt nach Kepler die empfindende Seele von Erde und Mensch den Einfallswinkel von Sonne, Mond und Sternen auf und reagiert entsprechend harmonisch. Ein Winkel am Kreis der Ekliptik (Ebene der Planeten) entspricht dabei der Teilung einer Saite.
Keplers Auffassung nach kann eine harmonische und eine disharmonische Stellung der Gestirne auf Anlage und Temperament fördernd bzw. hemmend einwirken; sie stellt gewissermaßen die Musik dar, nach der die Seele „tanzen“ muss.
Er verwendet das Notensystem, um zu beweisen, dass die sechs Planeten zusammen eine Harmonie ergeben, wenn man ihre Verhältnisse zueinander in das Notensystem überträgt.
Da Kepler die Vorstellung der Pythagoreer von der Sphärenharmonie und die Idee einer Planetentonleiter endlich auch mathematisch beweisen wollte, begann er nach Harmonien in den Bewegungen und Entfernungen der Planeten zu suchen. Die Umlaufszeiten im Verhältnis zueinander ergaben keine harmonischen Proportionen.
Schließlich betrachtete Kepler die extremen Winkelgeschwindigkeiten (die zeitliche Änderung des Drehwinkels bei einer Kreisbewegung, also die Ableitung des Winkels nach der Zeit) der Planeten von der Sonne aus gesehen, also die maximalen und minimalen Tagebögen der Planeten am „Sonnenhimmel“.
Diese ins Verhältnis zueinander gesetzt ergeben in fast allen Fällen vollkommene Harmonien.
| Saturn | Aphel a Perihel b |
a:b = 4:5 Große Terz a:d = 1:3 Zwölf Ganztöne c:d = 5:6 Kleine Terz |
| Jupiter | Aphel c Perihel d |
b:c = 1:2 Oktav c: f = 1:8 Drei Oktaven e: f = 2:3 Reine Quint |
| Mars | Aphel e Perihel f |
d:e = 5:24 Kleine Terz + zwei Oktaven e:h = 5:12 Kleine Terz + eine Oktav |
| Erde | Aphel g Perihel h |
g:h = 15:16 Diatonischer Halbton f:g = 2:3 Reine Quint g:k = 3:5 Große Sext |
| Venus | Aphel i Perihel k |
i:k = 24:25 Chromatischer Halbton h:i = 5:8 Kleine Sext i:m = 1:4 Doppeloktav |
| Merkur | Aphel l Perihel m |
l:m = 5:12 Kleine Terz + Oktav k:l = 3:5 Große Sext |
Die Verhältnisse zwischen den minimalen (im Aphel) und maximalen (im Perihel) Winkelgeschwindigkeiten einzelner und verschiedener Planeten von der Sonne aus gesehen.
[Das Perihel ist der sonnennächste, das Aphel der sonnenfernste Punkt einer Planetenbahn]
Beispiel:

Distanz von der Sonne (Erde-Sonne: 1000)

Die Abweichungen der 1989 gemessenen Planetenbewegungen von der Forderung der reinen Harmonie sind so klein, dass in den meisten Fällen das menschliche Ohr das aus der Planetenbewegung errechnete musikalische Intervall von dem reinen Intervall nicht unterscheiden kann.
So vergleicht Kepler dann, die von ihm entdeckten Harmonien der Planeten mit der Entdeckung des mehrstimmigen figurierten Gesangs, der damals erst wenige Jahrhunderte alt war:
„Wie sich der einfache oder einstimmige Gesang, den man Choralgesang nennt und der allein den Alten bekannt war, zum mehrstimmigen, sogenannten figurierten Gesang verhält, der eine Erfindung der letzten Jahrhunderte ist, so verhalten sich auch die Harmonien, die die einzelnen Planeten bilden, zu den Harmonien der Planetenpaare.“
Die von Kepler bezeichneten 7 Urharmonien der gespannten und geteilten Saite können somit auf der Sonne durch das Licht der Planeten wahrgenommen werden.
Denn Kepler sagt, dass von der Sonne als dynamischem Zentrum eine Kraft ausgehe. Diese Kraft würde alle Planeten auf elliptischen Bahnen bewegen (1.Gesetz). Elliptische Bahnen ergeben darüberhinaus sich ändernde Abstände und wechselnde Geschwindigkeiten der Planeten (2. Gesetz). Durch diesen Wechsel jedoch werden die gefundenen Harmonien erst möglich.
So folgert Kepler:
„Es sind also die Himmelsbewegungen nichts anderes als eine fortwährende, mehrstimmige Musik (durch den Verstand, nicht das Ohr fassbar), eine Musik, die durch dissonierende Spannungen, gleichsam durch Synkopen und Kadenzen hindurch (wie sie die Menschen in Nachahmung jener natürlichen Dissonanzen anwenden) auf bestimmte, vorgezeichnete, je sechsgliedrige (gleichsam sechsstimmige) Klauseln lossteuert und dadurch in dem unermesslichen Ablauf der Zeit unterscheidende Merkmale setzt. Es ist daher nicht mehr verwunderlich, dass der Mensch, der Nachahmer seines Schöpfers, endlich die Kunst des mehrstimmigen Gesangs, die den Alten unbekannt war, entdeckt hat. Er wollte die fortlaufende Dauer der Weltzeit in einem kurzen Teil einer Stunde mit einer kunstvollen Symphonie mehrerer Stimmen spielen und das Wohlgefallen des göttlichen Werkmeisters an seinen Werken soweit wie möglich nachkosten in dem so lieblichen Wonnegefühl, das ihm diese Musik in der Nachahmung Gottes bereitet“
Der Franzose Francis Warrain hat im Jahre 1942 Keplers Berechnungen überprüft und für richtig befunden. Er ermittelte auch harmonische Proportionen bei denen erst später entdeckten Planeten Uranus, Neptun und Pluto.
„Es ergaben sich mit den neuen Planeten 38 Intervalle, also 76 Töne, davon waren 22 Intervalle Urharmonien, 72 Töne gehören der Dur-Tonleiter an, 58 Töne entfallen auf den Dreiklang c{e{g , 44 Töne entfallen auf den Molldreiklang a{c{e.“
Die amerikanischen Professoren Rodgers und Ruff haben das Planetenorchester 1979 nach Keplers Anweisung auf dem Synthesizer nachgespielt. Ein Jahr wird hier zu wenigen Sekunden beschleunigt.
Vergleich Keplers „Komposition" 
Kepler:
„Die Planeten machten eine Art Musik, Harmonien die wir nur mit der Seele wahrnehmen können!“
I. Einleitung
Das Wort „Teleskop“ stammt ursprünglich aus dem griechischen. Es setzt sich aus zwei Worten zusammen.
tele (fern) und skopein (betrachten)
Warum benötigt man ein Teleskop?
Wie die Übersetzung des Namens schon sagt, dient es um in die Ferne sehen zu können. Es gibt Bereiche wie zum Beispiel die Astronomie, welche aufgrund der gegebnen Umstände und der enormen Entfernungen zwangsläufig auf Beobachtungen aus der Ferne angewiesen sind. Man kann in der Astronomie nicht so nah an ein Geschehen herantreten, dass man alle Details erkennen kann. Wir sind durch die Leistung unserer Augen in bestimmter Weise eingeschränkt. Diese sind allgemeine Werkzeuge unseres Körpers. Leider haben sie eine minimale Vergrößerungskapazität, eine limitierte Auflösung und auch eine Begrenzung des Lichteinfalls. So sind wir, wenn wir die Leistungsfähigkeit unserer Augen verbessern wollen auf optische Hilfsmittel wie zum Beispiel Brillen, Ferngläser oder Teleskope angewiesen. Das Teleskop ein optisches Hilfsmittel, welches sehr ferne Gegenstände vergrößert darstellen kann. Es zeigt einen kleinen Ausschnitt und vergrößert die darin enthaltenen fernen Objekte.
Geschichte
 Leider kann man den genauen Zeitpunkt der Erfindung des Teleskops nur sehr vage angeben. Ähnlich verhält es sich bei der Frage nach dem Erfinder. Grundsätzlich kann man sagen, dass für diese Rolle sehr viele Astronomen in Frage kommen. In diesem Zusammenhang werden sehr häufig Namen wie Galileo Galilei, Simon Marius so wie Thomas Harriot genannt.
Leider kann man den genauen Zeitpunkt der Erfindung des Teleskops nur sehr vage angeben. Ähnlich verhält es sich bei der Frage nach dem Erfinder. Grundsätzlich kann man sagen, dass für diese Rolle sehr viele Astronomen in Frage kommen. In diesem Zusammenhang werden sehr häufig Namen wie Galileo Galilei, Simon Marius so wie Thomas Harriot genannt.
Diese Astronomen haben es zwar nicht mit Sicherheit erfunden, sicher ist nur, dass sie die ersten Menschen waren, die das Fernrohr zum Himmel richteten, und das spielte sich um die Jahre 1609/1610 herum ab.
Galilei geriet mit Marius sogar in einen Streit, weil jeder von ihnen jeweils behauptete, die vier hellsten Jupitermonde als erster gesehen zu haben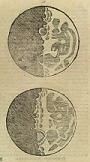
Galilei sichtete diese erstmalig im Januar 1610, was eindeutig belegt ist. Das Bild links zeigt seine Zeichnung, die er in Folge seiner Entdeckung anfertigte. Marius behauptete, die Jupitermonde früher gesehen zu haben, was letztlich nicht nachweisbar ist. So wird Galilei für gewöhnlich als Entdecker der vier hellsten Jupitermonde geführt, obwohl es Hinweise darauf gibt, dass Harriot die Monde noch vor Galilei und Marius gesehen, aber ihre wahre Natur nicht erkannt hat.
Mittlerweile glaubt man aber daran, dass die wirkliche Erfindung ein Holländer namens Johannes Lippershey machte. Dies soll mit großer Wahrscheinlichkeit um das Jahr 1608 erfolgt sein. Er war von Beruf Brillenmacher.
1609 entwickelte Galilei ein zusammengesetztes Mikroskop, welches aus einer konvexen (=nach außen gewölbt) und einer konkaven (= nach innen gewölbt) Linse bestand. Diese verbesserte und verfeinerte Version Lippersheys, von ihm "Occhiolino" genannt, schenkte er 1612 dem polnischen König Sigismund III.
II. Wirkungsweise
Definitionen
Sammellinse (auch Konvexlinse, Positivlinse) = ist eine Linse mit positiver, vergrößernder Brechkraft. Die Sammellinse sammelt das Licht und fokussiert es in ihrem Brennpunkt.
Brennpunkt = der Punkt, in dem eine optische Linse oder ein Hohlspiegel alle parallelen Lichtstrahlen sammelt
Brennweite = Abstand zwischen Objektiv und Brennpunkt
Objektiv = Ein Objektiv ist ein sammelndes optisches System, das eine reelle optische Abbildung eines Objektes erzeugt
Okular = eine Linse oder Linsensystem, durch das man mit dem Auge (lat. oculus) in ein optisches System blickt
Die allgemeine Wirkungsweise von Teleskopen
Man bündelt parallel einfallende Lichtstrahlen mit Hilfe eines Objektivs in einem Punkt, dem so genannten Fokalpunkt (Brennpunkt). Das Objektiv, also das Licht sammelnde Medium, das dem zu beobachtenden Objekt zugewandt ist, ist eine bikonvexe, also beidseitig erhabene Glaslinse. Diese Strahlen werden sodann von einer Linse oder einer Gruppe von Linsen, Okular genannt, vergrößert. Dieses Okular wird hinter dem Brennpunkt platziert. Der Durchmesser des zu beobachtenden Gebietes richtet sich nach dem Gesichtsfeld des verwendeten Okulars.
Das eigentliche astronomische Fernrohr wurde von Johannes Kepler entwickelt und beschrieben, weshalb man bis heute vom Keplerschen Fernrohr spricht. Es benutzt als Okular eine bikonvexe Linse. Dieses Teleskop entwirft auf dem Kopf stehende Bilder. Sämtliche heutigen Linsenteleskope vom Amateurinstrument bis zum professionellen Sternwartengerät beruhen auf dem Prinzip des Keplerschen Fernrohrs. Da die Bilderzeugung bei dieser Teleskopart auf Brechung ("Refraktion") beruht, spricht man auch von einem "Refraktor".
III. Refraktor - Reflektor
Es gibt grundsätzlich zwei Arten, Licht zu bündeln:
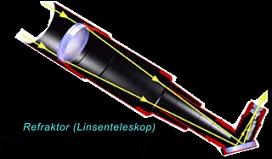
- Man schickt die Lichtstrahlen durch eine oder mehrere Linsen, "gebogene" und polierte "Glasscheiben". Das Gerät wird aufgrund der Lichtbrechung als Refraktor bezeichnet.
- Man verwendet zum Sammeln des Lichts einen gekrümmten Spiegel. Das am meisten verbreitete Design ist der Newton-Reflektor, benannt nach seinem Erfinder Isaac Newton.
1.) Refraktor
Nach dem Konstruktionsprinzip unterscheidet man das Galilei-Fernrohr oder holländische Fernrohr vom Kepler-Fernrohr oder astronomischen Fernrohr.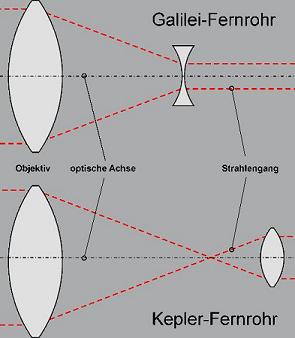
Galilei-Fernrohr
Das Galilei-Fernrohr hat als Objektiv eine Sammellinse und als Okular eine Zerstreuungslinse kleinerer Brennweite. Es besitzt ein kleines Gesichtsfeld, stellt die Objekte aber aufrecht und seitenrichtig dar. Es ist heute nur noch als Opernglas und als fest installiertes Aussichtsfernrohr in Gebrauch.
Kepler-Fernrohr
Beim Kepler-Fernrohr werden sowohl für das Objektiv als auch für das Okular Sammellinsen verwendet. Die Vergrößerung eines Refraktors ergibt sich aus dem Verhältnis der Brennweiten des Objektivs und des Okulars. Ein Gerät mit 1.000 mm Objektiv-Brennweite und 5 mm Okular-Brennweite besitzt somit eine 200fache Vergrößerung.
Der Unterschied ist hauptsächlich im Strahlengang erkennbar
Vorteile:
- Staub und Schmutz kann aufgrund der geschlossenen Optik nicht eindringen
- Optik ist in sich geschlossen und benötigt keine regelmäßige Justierung
- System hat keine zentrale Abschattung die den Lichteinfall schwächt und das Beugungsbild einschränken kann
Problem:
Durch die unterschiedlichen Brennpunkten der verschiedenen Wellenlängen, können sich um helle Objekte Farbsäume bilden. Deswegen muss mit zusätzlichen Linsen oder speziellem Glas entgegengewirkt werden. Dies erfordert aber meist eine Sonderanfertigung und das ist sehr teuer
Reales Beispiel:


2.) Reflektor
 Ein Spiegel wird durch Beschichtung eines konkaven Glases mit einer reflektierenden Schicht hergestellt. Das auftreffende Licht wird von der Oberfläche reflektiert und im Brennpunkt vereinigt. Da es keine Linsen durchläuft, produziert ein Spiegelteleskop auch keine Farbfehler.
Ein Spiegel wird durch Beschichtung eines konkaven Glases mit einer reflektierenden Schicht hergestellt. Das auftreffende Licht wird von der Oberfläche reflektiert und im Brennpunkt vereinigt. Da es keine Linsen durchläuft, produziert ein Spiegelteleskop auch keine Farbfehler.
Leider wirkt das Konzept nur bei Spiegeln mit Öffnungsverhältnis f/9 oder länger. Bei größeren Spiegeln (ab 150mm) oder kurzen Brennweiten unter f/8 wird das Licht von dieser Art von Spiegeln jedoch nicht exakt in exakt in einem Punkt vereinigt.
Die sphärische Abweichung entsteht, wenn Lichtstrahlen von Rand des Spiegels in einem anderen Brennpunkt als Strahlen von zentraleren Spiegelteilen eintreffen. Zur Bewältigung dieses Problems verwendet man Spiegel mit einer gekrümmten Form.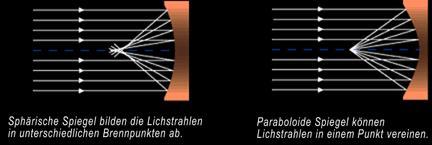
Vorteile:
- nur zwei optische Oberflächen müssen bearbeitet und poliert werden, das macht es preiswerter in der Produktion
- keine Farbfehler, da das Licht keine Linse durchläuft
Nachteile:
- lange Tuben aufgrund von längerer Brennweite, das macht das Teleskop viel anfälliger gegen Wind als andere Designs
- Durch die Stellung des Spiegels im Strahlengang gibt es eine Bildverschlechterung und Lichtverlust. Das Licht muss an den Metallstreben die den Spiegel befestigen, vorbei, dies führt zu einem Qualitätsverlust des Lichtes
Reales Beispiel:


IV. Bedeutende Großteleskope in der Geschichte
 William Herschel (1738-1822) baute die größten Teleskope seiner Zeit und wurde vor allem durch die Entdeckung des Uranus 1781 bekannt. Aber er versuchte auch als einer der ersten Astronomen, die Struktur der Milchstraße zu ergründen.
William Herschel (1738-1822) baute die größten Teleskope seiner Zeit und wurde vor allem durch die Entdeckung des Uranus 1781 bekannt. Aber er versuchte auch als einer der ersten Astronomen, die Struktur der Milchstraße zu ergründen.
 Im Observatorium des amerikanischen Astronomen Percival Lowell (1855-1916) in Flagstaffs, gibt es einen Refraktor mit einem Objektivdurchmesser von 61 Zentimetern.
Im Observatorium des amerikanischen Astronomen Percival Lowell (1855-1916) in Flagstaffs, gibt es einen Refraktor mit einem Objektivdurchmesser von 61 Zentimetern.
Bekannt geworden ist Lowell vor allem durch seine Marsbeobachtungen und seine Suche nach dem "Planeten X", dem Transneptun.
Das Lick-Observatorium auf dem 1283 Meter hohen Mount Hamilton unweit der kalifornischen Stadt San José besitzt einen Refraktor mit einem Objektivdurchmesser von 90 cm.(links)
 Das bis heute größte Linsenfernrohr der Erde wurde 1897 am Lake Geneva im amerikanischen Bundesstaat Wisconsin in der Nähe von Chicago eingeweiht. Nach dessen Sponsor Charles Tyson Yerkes (1837-1905) spricht man bis heute vom Yerkes-Observatorium. Dessen Objektiv mit einem Durchmesser von 102 Zentimetern war auch aus dem Hause Clark(unten)
Das bis heute größte Linsenfernrohr der Erde wurde 1897 am Lake Geneva im amerikanischen Bundesstaat Wisconsin in der Nähe von Chicago eingeweiht. Nach dessen Sponsor Charles Tyson Yerkes (1837-1905) spricht man bis heute vom Yerkes-Observatorium. Dessen Objektiv mit einem Durchmesser von 102 Zentimetern war auch aus dem Hause Clark(unten)
 Das Konstruieren von Fernrohren hatte lange Zeit einen wettbewerbsähnlichen Charakter. Denn es gab viel zu entdecken im All. Jedoch ist vermutlich eine Objektivlinse mit einem Durchmesser von einem Meter das Limit. Denn noch größere Linsen würden sich aufgrund ihres Eigengewichtes durchbiegen, da sie ja auch nur an ihren Rändern abgestützt werden können. Denn es ist ja die Absicht, dass möglichst viel Licht, das durch die linse fällt, genutzt wird. Dieses Problem gibt es bei Spiegeln nicht, denn hier gibt es bloß eine optisch wirksame Fläche, die reflektiert, und das Medium, der Spiegel also, kann über seinem vollständigen Durchmesser an der optisch unwirksamen Seite abgestützt werden.
Das Konstruieren von Fernrohren hatte lange Zeit einen wettbewerbsähnlichen Charakter. Denn es gab viel zu entdecken im All. Jedoch ist vermutlich eine Objektivlinse mit einem Durchmesser von einem Meter das Limit. Denn noch größere Linsen würden sich aufgrund ihres Eigengewichtes durchbiegen, da sie ja auch nur an ihren Rändern abgestützt werden können. Denn es ist ja die Absicht, dass möglichst viel Licht, das durch die linse fällt, genutzt wird. Dieses Problem gibt es bei Spiegeln nicht, denn hier gibt es bloß eine optisch wirksame Fläche, die reflektiert, und das Medium, der Spiegel also, kann über seinem vollständigen Durchmesser an der optisch unwirksamen Seite abgestützt werden.
