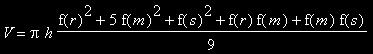I. Einleitung
Wie kam es zur Fassregel?
Auf die Idee, sich mit der Berechnung von Flächeninhalten unter einer Fasskurve und dem entsprechenden Fassvolumen zu befassen, kam Johannes Kepler, als er einige Fässer Wein, die er für seine zweite Hochzeit brauchte, bezahlen musste. Er erkannte dabei, dass der Preis, welcher sich nach dem Volumen des Fasses richtete, auf Grund von Ungenauigkeiten beim Errechnen des Volumens des gefüllten Fasses nicht exakt war. Bis dahin war es üblich, das Volumen von Fässern mit der Visiermethode zu bestimmen. Diese ließ jedoch außer Acht, dass nicht jedes Fass mit denselben Proportionen gebaut wurde. Demnach kann ein sehr hohes Fass mit schmalen Böden denselben Rauminhalt wie ein niedrigeres Fass mit breiteren Böden haben. Außerdem beauftragte der Magistrat der Stadt Ulm Kepler 1615, neue Maßeinheiten für die Stadt festzulegen.
Zitat von Kepler:
"Als einige Fässer eingekellert waren, kam am 4.Tag der Verkäufer mit der Messrute, mit der er alle Fässer, ohne Rücksicht auf ihre Form, ohne jede weitere Überlegung oder Rechnung ihrem Inhalte nach bestimmte. Die Visierrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden geführt, und als die beiden Längen gleich gefunden worden waren, ergab die Marke am Spundloch die Zahl der Eimer im Fasse. Ich wunderte mich, dass die Querlinie durch die Fasshälfte ein Maß für den Inhalt abgeben könne, und bezweifelte die Richtigkeit der Methode, denn ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Inhalt könnte dieselbe Visierlänge besitzen.
Es schien mir als Neuvermähltem nicht unzweckmäßig, ein neues Prinzip mathematischer Arbeiten, nämlich die Genauigkeit dieser bequemen und allgemein wichtigen Bestimmung nach geometrischen Grundsätzen zu erforschen und die etwa vorhandenen Gesetze ans Licht zu bringen."
Wozu dient die Keplersche Fassregel?
Mit Hilfe der Keplerschen Fassregel ist es näherungsweise möglich ohne Integralrechnung die Fläche unter einer Kurve zu bestimmen.
Die Keplersche Fassregel basiert auf recht einfachen Größen: der Höhe h des Fasses, dem Radius des Deckels, dem Radius des Bodens und dem Radius auf halber Höhe des Fasses.
Den Deckelradius nennen wir f(r), den Mittelradius f(m) und den Bodenradius f(s) (Die komisch anmutenden Benennungen resultieren aus der Herleitung der Keplerschen Fassregel, die später noch genauer aufgezeigt wird). Dann ergibt sich nach Kepler die relativ einfache Regel zur Bestimmung der Querschnittsfläche A eines Fasses, die sogenannte "Keplersche Fassregel".
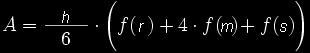
Außerdem erhält man näherungsweise, aber relative genau, das Volumen eines Fasses: