Seite 4 von 5
IV. Anwendungsmöglichkeiten
Mit Hilfe der Keplerschen Fassregel kann man mit relativ wenig Aufwand eine krummlinig begrenzte Fläche A im Intervall [a,b] ermitteln.
Dazu ersetzt man den Funktionsgraphen durch eine Parabel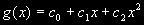 
, die den Funktionsgraphen f(x) in den drei Punkten P0, P1, P2 schneidet.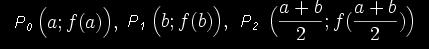 
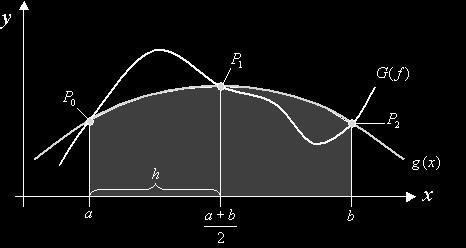
Die drei Funktionswerte erhält man, indem man a, [(a+b)/2) und b in die Parabelgleichung einsetzt.
Jetzt muss man diese nur noch in die Formel zur Keplerschen Fassregel einsetzen.
Weitere Anwendungsmöglichkeiten u.a.:
Berechnung von...
...Kreisflächen
...Fläche unter der Sinuskurve
...Fläche unter der Parabel
...Kegeln (-stumpfe)
...Kugeln
...Rotationsparaboloiden ( = Rotationskörper einer Parabel )