III. Mängel der Regel / Visiermethode
Mängel der Keplerschen Fassregel
Je nach Faßform ist die Keplersche Faßregel mehr oder weniger ungenau, da es sich nur um eine Näherungsformel handelt. Aber verglichen mit der geringeren Genauigkeit der Visiermethode und dem größeren mathematischen Aufwand der Integralrechnung dürfte die Keplersche Fassregel wohl die praktischste aller Lösungen sein. Zur Berechnung benötigt man nur vier Größen; diese sind dazu noch recht leicht zu ermitteln: den Radius des Deckels, den des Bodens und den des Faßbauches auf halber Höhe, schließlich noch die Höhe des Fasses. Und für diesen geringen Aufwand beweist die Keplersche Faßregel eine erstaunliche Genauigkeit, die Abweichung liegt, zumindest bei faßähnlichen Gebilden, meistens im Promille-Bereich. Dieser Fehler ist jedenfalls kleiner als die durch genaues oder ungenaues Füllen des Fasses entstehenden Unterschiede!
Mängel der Visiermethode
Bedenkt man nur die zu messenden Größen, so erscheint die Visiermethode mit nur einer solcher Größe, nämlich den Abstand vom Spundloch in die tiefste Bodenecke, sehr leicht anwendbar. Zwar ist die erzielte Genauigkeit recht groß, wenn man die Einfachheit der Methode bedenkt, aber dennoch - insbesondere im Vergleich mit den anderen hier vorgestellten Methoden - nicht zufriedenstellend.
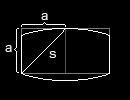
Der Hauptmangel der Visiermethode ist in der Herleitung deutlich zu erkennen: Man geht von einer bestimmten Fassform aus, bei der die Oberseite und die Unterseite gleich lang, die Verlängerung der Oberseite bis über am weitesten ausgewölbten Punkt des Fassbauches genauso lang ist wie die halbe Höhe des Fasses.
Darüber hinaus wird, ebenfalls in der Herleitung erkennbar, aufgerundet: 0,5555...s³ wird gerundet zu 6s³.
Ob sich diese beiden Rundungen gegenseitig aufheben oder eher verschlimmern, hängt von der endgültigen Form des einzelnen Fasses ab. Wie sehr sich diese Rundungen bemerkbar machen, zeigt der Genauigkeitsvergleich der einzelnen Methoden.
Herleitung der Visisermethode:
Ersetzt man das Fass durch einen Zylinder, dessen Durchmesser halb so groß wie seine Höhe ist so gilt für sein Volumen folgendes:
allgemein: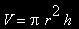
für diesen Fall: 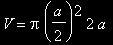
(wobei "(a/2)" den halben Durchmesser und somit den Radius der Grundseite darstellt).
Und da s² = 2a² (nach Pythagoras), folgt:
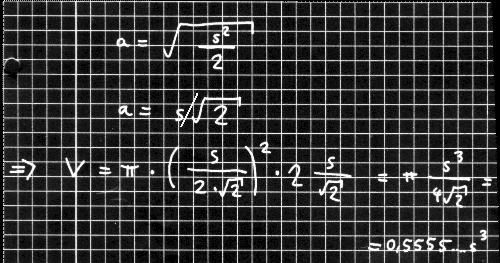
Man kann also ungefähr sagen V = 0,6 s³
Dieser letzte Term entspricht genau der Visiermethode.
Wie man hier sieht, ist neben der Abweichung der Formen noch eine Ungenauigkeit beim Aufrunden vorhanden, daher ist die Visiermethode gerade in puncto Genauigkeit mit erheblichen Mängeln versehen.
