I. Einleitung
Wie kam es zur Fassregel?
Auf die Idee, sich mit der Berechnung von Flächeninhalten unter einer Fasskurve und dem entsprechenden Fassvolumen zu befassen, kam Johannes Kepler, als er einige Fässer Wein, die er für seine zweite Hochzeit brauchte, bezahlen musste. Er erkannte dabei, dass der Preis, welcher sich nach dem Volumen des Fasses richtete, auf Grund von Ungenauigkeiten beim Errechnen des Volumens des gefüllten Fasses nicht exakt war. Bis dahin war es üblich, das Volumen von Fässern mit der Visiermethode zu bestimmen. Diese ließ jedoch außer Acht, dass nicht jedes Fass mit denselben Proportionen gebaut wurde. Demnach kann ein sehr hohes Fass mit schmalen Böden denselben Rauminhalt wie ein niedrigeres Fass mit breiteren Böden haben. Außerdem beauftragte der Magistrat der Stadt Ulm Kepler 1615, neue Maßeinheiten für die Stadt festzulegen.
Zitat von Kepler:
"Als einige Fässer eingekellert waren, kam am 4.Tag der Verkäufer mit der Messrute, mit der er alle Fässer, ohne Rücksicht auf ihre Form, ohne jede weitere Überlegung oder Rechnung ihrem Inhalte nach bestimmte. Die Visierrute wurde mit ihrer metallenen Spitze durch das Spundloch quer bis zu den Rändern der beiden Böden geführt, und als die beiden Längen gleich gefunden worden waren, ergab die Marke am Spundloch die Zahl der Eimer im Fasse. Ich wunderte mich, dass die Querlinie durch die Fasshälfte ein Maß für den Inhalt abgeben könne, und bezweifelte die Richtigkeit der Methode, denn ein sehr niedriges Fass mit etwas breiteren Böden und daher sehr viel kleinerem Inhalt könnte dieselbe Visierlänge besitzen.
Es schien mir als Neuvermähltem nicht unzweckmäßig, ein neues Prinzip mathematischer Arbeiten, nämlich die Genauigkeit dieser bequemen und allgemein wichtigen Bestimmung nach geometrischen Grundsätzen zu erforschen und die etwa vorhandenen Gesetze ans Licht zu bringen."
Wozu dient die Keplersche Fassregel?
Mit Hilfe der Keplerschen Fassregel ist es näherungsweise möglich ohne Integralrechnung die Fläche unter einer Kurve zu bestimmen.
Die Keplersche Fassregel basiert auf recht einfachen Größen: der Höhe h des Fasses, dem Radius des Deckels, dem Radius des Bodens und dem Radius auf halber Höhe des Fasses.
Den Deckelradius nennen wir f(r), den Mittelradius f(m) und den Bodenradius f(s) (Die komisch anmutenden Benennungen resultieren aus der Herleitung der Keplerschen Fassregel, die später noch genauer aufgezeigt wird). Dann ergibt sich nach Kepler die relativ einfache Regel zur Bestimmung der Querschnittsfläche A eines Fasses, die sogenannte "Keplersche Fassregel".
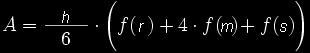
Außerdem erhält man näherungsweise, aber relative genau, das Volumen eines Fasses:
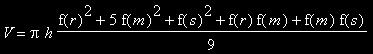
II. Herleitung
Wie kann man der Keplerschen Fassregel mathematischen Halt verleihen?
Nun, stellen wir uns zunächst vor, das Fass wäre eine einfache Tonne, hätte also einen geraden anstatt eines gewölbten seitlichen Randes. Dann wäre das Volumen dieses Körpers einfacher zu berechnen, nämlich als das Produkt aus der kreisförmigen Grundfläche A und der Höhe h.
Die Grundfläche wiederum ergibt sich aus dem Produkt des Quadrats des Radius r mit der Kreiszahl Pi: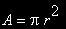 
Das Volumen V wäre demnach: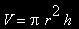 
Wie aber berechnet sich das Volumen eines Fasses, das ja einen Bauch und keinen geraden Rand hat?
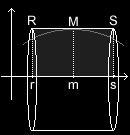
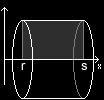Wir bedienen uns eines einfachen, in der Mathematik oft angewandten Tricks: Wir reduzieren das Problem zunächst auf ein einfacheres, eines welches wir schon ohne große Mühe lösen können, nämlich auf die oben erwähnte Tonne; allerdings betrachten wir unsere Tonne nun auf eine andere Weise: wir stellen sie nicht mehr auf, sondern wir legen sie auf die Seite, oder noch besser: wir hängen sie entlang ihrer Mitte auf, so dass die Seiten nun parallel zum Boden liegen. Zum Aufhängen benutzen wir keine Schnur, sondern die x-Achse eines Koordinatensystems zwischen den Stellen r (Mitte des Fassdeckels) und s (Mitte des Fassbodens). Den Anfangs- und den Endpunkt des Bogens nennen wir entsprechend R bzw. S.
Den Radius r der Tonne drücken wir über eine Funktion f aus, dann errechnet sich das Volumen nun als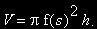 
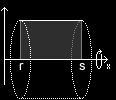Stellen wir uns die Tonne aber einmal nicht als aufgehängten Körper vor, sondern als den Raum, den ein um die x-Achse rotierendes Rechteck, dessen unterer Rand die x-Achse und dessen oberer Rand die Strecke RS bildet, einnimmt. So merken wir schnell, dass es die Fläche des Rechteckes ist, die das Volumen des Rotationskörpers", also in unserem Falle des Fasses, bestimmt. Die sogenannte Keplersche Fassregel" gibt uns den Inhalt solcher Flächen an.
Wie ersetzen wir unsere Tonne nun wieder durch das Fass?
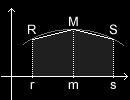Gerade dabei ergibt sich allerdings ein Problem: Mit einer geeigneten Funktion f können wir zwar leicht den gewölbten Rand des Fasses nachzeichnen, um so zu einer geeigneten Rotationsfläche zu gelangen. f(x) gibt uns den Radius des Fasses aber nur an einer einzigen Stelle (nämlich an der Stelle x) an. Daher unterteilen wir den Bogen, den die Funktion f nachzeichnet, in zwei Abschnitte. Idealerweise wählen wir die halbe Höhe des Fasses als Trennstelle, die Stelle nennen wir m, den entsprechenden Punkt auf dem Bogen (bzw. dem Fassrand) nennen wir M. Dann verbinden wir die Punkte R und M sowie M und S jeweils durch Strecken, um den Bogen grob schematisiert nachzeichnen zu können.
Zwar verlieren wir durch die "Schematisierung" (man sagt in der Mathematik: "Approximation" oder "Annäherung an die Kurve") an Genauigkeit, dafür können wir die erhaltene Rotationsfläche des manipulierten Fasses leicht errechnen: Beide Abschnitte stellen je ein Trapez dar, dessen Flächeninhalt A gleich dem Produkt aus der Länge der Grundseite, also in unserem Fall der halben Höhe h des (stehenden) Fasses, und der mittleren Höhe des Trapezes. 
Analog erhalten wir für den zweiten Abschnitt den Flächeninhalt: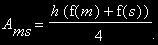 
Beide zusammen ergeben die Rotationsfläche der gesamten Figur: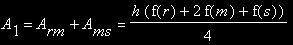 
Bei der Schematisierung ist die Rotationsfläche und damit auch unser Fass etwas zu klein geraten, da die Strecken RM und MS unterhalb des Bogens verlaufen.
Können wir diesen Fehler wieder etwas ausgleichen?
Als Ausgleich zu dem Verlust an Rotationsfläche, der bei der Schematisierung entstanden ist, gibt es ein weiteres Verfahren, mit dem man die Fläche unterhalb des Bogens ebenfalls schematisiert darstellt; hierbei wird die Fläche aber vergrößert, was als Ausgleich zum Verlust beim ersten Verfahren dienen soll: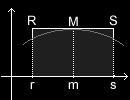 
Es ist einfacher, aber auch ungenauer als das erste Verfahren, denn wir wählen diesmal als Rotationsfläche einfach das Rechteck der Höhe f(m) zwischen den Stellen a und b, das also genau so lang ist wie das (stehende) Fass hoch; der Flächeninhalt dieses Rechtecks ist demnach: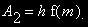 
Es bleibt die Frage, wie wir beide Verfahren miteinander kombinieren sollen.
Nun, da das erste Verfahren um den Faktor 2 genauer ist, denn hier haben wir das Fass zur Schematisierung in zwei Abschnitte unterteilt, verrechnen wir es einfach mit dem zweiten, bei dem wir das gesamte Fass sozusagen in einem Abschnitt schematisiert haben, in der Wertigkeit 2 zu 1: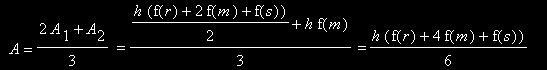 
Bei der erhaltenen Näherungsformel handelt es sich um die "Keplersche Fassregel".
Um aber das Volumen eines Fasses zu berechnen, müssen wir noch weiter überlegen, denn diese Keplersche Fassregel gibt uns ja offensichtlich nur die halbe Querschnittsfläche eines Fasses an, nicht aber dessen Volumen.
Wie berechnet man also das Volumen nach Kepler?
Nun, wir vollziehen wieder jeden Schritt beider Näherungen nach: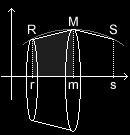 
Bei der ersten Näherung erhalten wir zwei Trapeze. Lassen wir diese um die x-Achse rotieren, so erhalten wir je einen Kegelstumpf. Das Volumen eines Kegelstumpfes erhält man aus, wobei R und r die Radien, h die Höhe des Kegelstumpfes sind :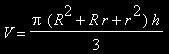 
Bei unseren beiden Trapezen wären das also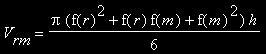 
und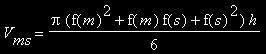 
Beide zusammen ergeben wieder unsere erste Näherung: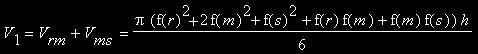 
Um die zweite Näherung zu erhalten, lassen wir das umschriebene Rechteck rotieren und bekommen so einen Zylinder bzw. eine Tonne. Deren Flächeninhalt errechnet sich als 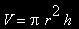, wobei r der Radius und h die Höhe ist. In unserem Beispiel wäre f(m) der Radius, das Volumen der zweiten Näherung folglich :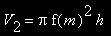 
Verrechnen wir wieder beide Näherungen in der Wertung 2:1 miteinander, so erhalten wir als endgültige Näherung für das Volumen :
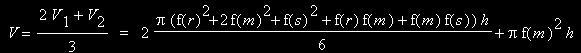
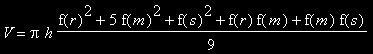
Für den Spezialfall f(r) = f(s) ergibt sich dann:
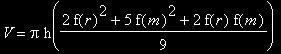
III. Mängel der Regel / Visiermethode
Mängel der Keplerschen Fassregel
Je nach Faßform ist die Keplersche Faßregel mehr oder weniger ungenau, da es sich nur um eine Näherungsformel handelt. Aber verglichen mit der geringeren Genauigkeit der Visiermethode und dem größeren mathematischen Aufwand der Integralrechnung dürfte die Keplersche Fassregel wohl die praktischste aller Lösungen sein. Zur Berechnung benötigt man nur vier Größen; diese sind dazu noch recht leicht zu ermitteln: den Radius des Deckels, den des Bodens und den des Faßbauches auf halber Höhe, schließlich noch die Höhe des Fasses. Und für diesen geringen Aufwand beweist die Keplersche Faßregel eine erstaunliche Genauigkeit, die Abweichung liegt, zumindest bei faßähnlichen Gebilden, meistens im Promille-Bereich. Dieser Fehler ist jedenfalls kleiner als die durch genaues oder ungenaues Füllen des Fasses entstehenden Unterschiede!
Mängel der Visiermethode
Bedenkt man nur die zu messenden Größen, so erscheint die Visiermethode mit nur einer solcher Größe, nämlich den Abstand vom Spundloch in die tiefste Bodenecke, sehr leicht anwendbar. Zwar ist die erzielte Genauigkeit recht groß, wenn man die Einfachheit der Methode bedenkt, aber dennoch - insbesondere im Vergleich mit den anderen hier vorgestellten Methoden - nicht zufriedenstellend.
Der Hauptmangel der Visiermethode ist in der Herleitung deutlich zu erkennen: Man geht von einer bestimmten Fassform aus, bei der die Oberseite und die Unterseite gleich lang, die Verlängerung der Oberseite bis über am weitesten ausgewölbten Punkt des Fassbauches genauso lang ist wie die halbe Höhe des Fasses.
Darüber hinaus wird, ebenfalls in der Herleitung erkennbar, aufgerundet: 0,5555...s³ wird gerundet zu 6s³.
Ob sich diese beiden Rundungen gegenseitig aufheben oder eher verschlimmern, hängt von der endgültigen Form des einzelnen Fasses ab. Wie sehr sich diese Rundungen bemerkbar machen, zeigt der Genauigkeitsvergleich der einzelnen Methoden.
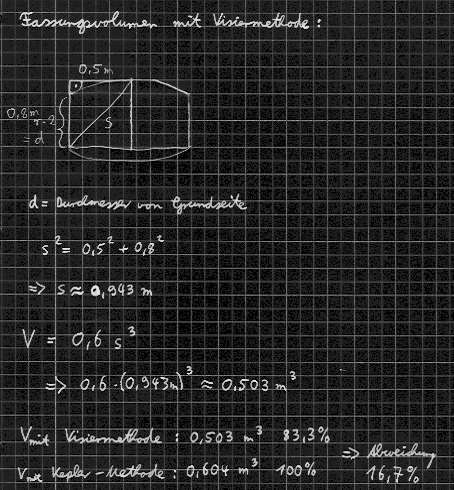
Herleitung der Visisermethode:
Ersetzt man das Fass durch einen Zylinder, dessen Durchmesser halb so groß wie seine Höhe ist so gilt für sein Volumen folgendes:
allgemein: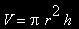
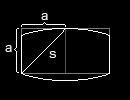
für diesen Fall: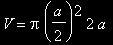 
(wobei "(a/2)" den halben Durchmesser und somit den Radius der Grundseite darstellt).
Und da s² = 2a² (nach Pythagoras), folgt:
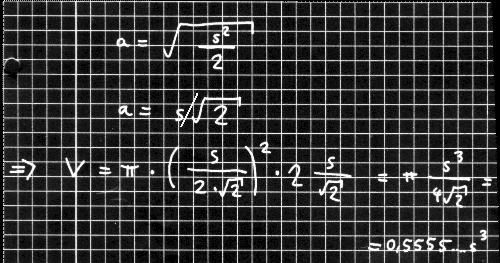
Man kann also ungefähr sagen V = 0,6 s³
Dieser letzte Term entspricht genau der Visiermethode.
Wie man hier sieht, ist neben der Abweichung der Formen noch eine Ungenauigkeit beim Aufrunden vorhanden, daher ist die Visiermethode gerade in puncto Genauigkeit mit erheblichen Mängeln versehen.
IV. Anwendungsmöglichkeiten
Mit Hilfe der Keplerschen Fassregel kann man mit relativ wenig Aufwand eine krummlinig begrenzte Fläche A im Intervall [a,b] ermitteln.
Dazu ersetzt man den Funktionsgraphen durch eine Parabel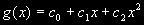 
, die den Funktionsgraphen f(x) in den drei Punkten P0, P1, P2 schneidet.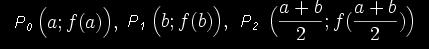 
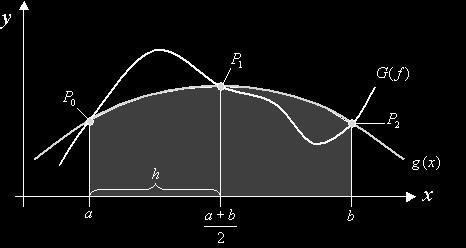
Die drei Funktionswerte erhält man, indem man a, [(a+b)/2) und b in die Parabelgleichung einsetzt.
Jetzt muss man diese nur noch in die Formel zur Keplerschen Fassregel einsetzen.
Weitere Anwendungsmöglichkeiten u.a.:
Berechnung von...
...Kreisflächen
...Fläche unter der Sinuskurve
...Fläche unter der Parabel
...Kegeln (-stumpfe)
...Kugeln
...Rotationsparaboloiden ( = Rotationskörper einer Parabel )
V. Beispiel-Aufgabe
Verfolgt man die Entwicklung der Rotationskörper historisch, so kommt man nicht umhin zu erkennen, dass am Anfang eine recht pragmatische Frage stand. Die Frage war: „Wie kann man das Volumen eines Weinfasses berechnen“.
Deshalb soll auch die hier vorgestellte Beispiel-aufgabe auf genau diese Ursprungsfragestellung zurückgehen:
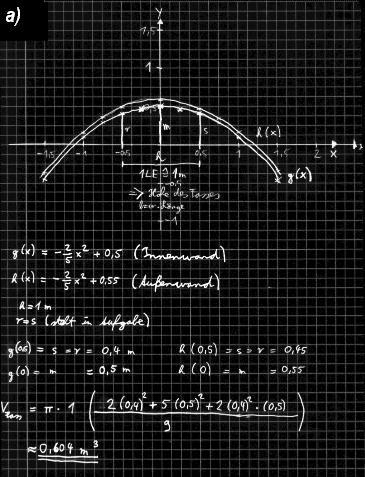
Die Innenwand unseres Fasses wird durch die Funktion f(x)= -(2/5)x^2+0,5.
Es hat eine Höhe von einem Meter und der Radius des Deckels und des Bodens stimmen überein.
Die Außenwand wird durch die Funktion f(x)= -(2/5)x^2+0,55 festgelegt (1LE entspricht 1m).
a) Bestimme die notwendigen Radien und überprüfe durch Berechnung des entsprechenden Rotationskörpers, ob mit der Fassregel das Volumen unseres Fasses näherungsweise berechnet werden kann.
b) Bestimme die Masse des leeren Holzfasses unter der Annahme, dass das verwandte Holz eine Dichte von 1070 (kg/m^3) hat.
Teilaufgabe a): Teilaufgabe b):
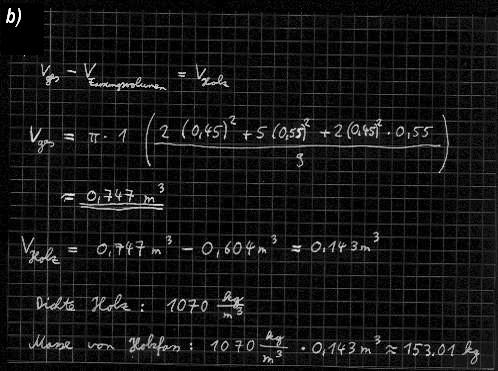
Ein Vergleich des errechneten Volumens mit dem Ergebnis das die Visiermethode ergibt:
