I. Einleitung
Teleskope müssen wendbar sein, wenn man den Himmel beobachten möchte, denn durch die Drehung und Bewegung der Erde und der zu beobachtenden Himmelserscheinungen, muss man immer wieder das Teleskop neu ausrichten können. Mit Montierung bezeichnet man den mechanischen Teil, der das eigentliche Teleskop trägt. Die Montierung dient dazu, die Erddrehung auszugleichen und so die Sterne im Teleskop während der Beobachtung oder Aufnahme punktförmig zu halten.
Um das grundlegende Prinzip an einem ganz einfachen Beispiel zu erläutern nehmen wir die sogenannte Freihand-Montierung als Beispiel:
Bei dieser Form hält man das Beobachtungsinstrument in den Händen. Der Körper selbst stellt die Drehachse und das Genick die Höhenachse dar. Durch Drehen des Körpers und durch das Schwenken des Kopfes kann man so das Gerät (und seien es nur die bloßen Augen) auf jeden beliebigen Punkt des Himmels ausrichten.
Grundsätzlich unterscheidet man bei Montierungen astronomischer Teleskope zwischen zwei Arten. Natürlich gibt es zu jeder Methode auch spezielle Untereinheiten.
- azimutale Montierung
- parallaktische oder äquatoriale Montierung
Die Namen basieren auf dem Koordinatensystem für das sie konzipiert sind.
II. Azimutale Montierung
Begriffsklärung
Bogensekunde = Ein Grad wird unterteilt in 60 Bogenminuten und jede Bogenminute wiederum in 60 Bogensekunden. Ein Grad entspricht also 3.600 Bogensekunden
Meridianebene = teilt die Himmelskugel in gleiche Hälften; in der Meridianebene erreichen alle Fixsterne ihre größte Höhe
Azimut = Winkel zwischen der Meridianebene und dem Schnittpunkt des Vertikalkreises eines Gestirns mit dem Horizont
Horizont = Der Horizont (griechisch = der Gesichtskreis) ist die Grenzlinie zwischen der sichtbaren Erde und dem Himmel
Der Name entlehnt sich aus dem azimutalen Koordinatensystem, welches manchmal auch als Horizontalkoordinatensystem bezeichnet wird.
Azimutales Koordinatensystem:
In diesem Koordinatensystem wird ein Punkt am Himmel über seinen Azimutwinkel (=Horizontalwinkel; der Horizont wird von Süd über West, Nord und Ost in 360 Grad eingeteilt wobei Süd gleich zu 0 Grad definiert ist) und über seine Winkelhöhe zwischen dem Horizont und dem Zenit (das ist der Punkt genau über dem Beobachter) festgelegt. Der Höhenwinkel beginnt am Horizont mit 0 Grad zu zählen und endet im Zenit bei +90 Grad.
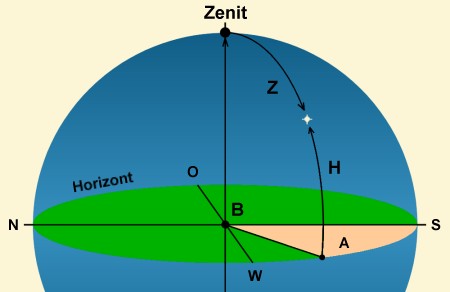
A = Azimutwinkel
H = Höhenwinkel (Manchmal verwendet man auch Z = Zenitalwinkel)
B steht für den Beobachter
Diese Montierungen bestehen aus zwei Drehachsen, die im rechten Winkel zueinander angeordnet sind. Die eine Achse ist die sogenannte Azimutachse und die zweite ist die Höhenachse. Die Azimut - oder auch Drehachse steht dabei senkrecht zur Erdoberfläche, die Montierungsausrichtung ist frei wählbar.
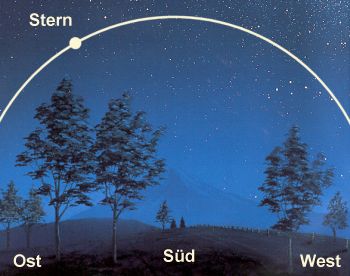Wenn man einen Stern die Nacht über beobachtet, wird man feststellen, dass er scheinbar eine „Wanderung“ von Ost nach West vollzieht, wobei er im Süden seinen höchsten Punkt erreicht.
Jedoch trügt hier der Schein, denn der Stern bleibt andauernd auf seiner Position. Die scheinbare Bewegung kommt durch die Eigendrehung der Erde zu Stande.
Daraus können wir schlussfolgern, dass wenn man die Koordinaten eines Himmelsobjekts im azimutalen Koordinatensystem angibt, auch noch eine Zeitinformation dazugehört, da sich beide Winkelangaben permanent aufgrund der Erdrotation ändern.
Wenn man eine relativ primitive Montierung besitzt, dann ist diese meist aus einer Gabel. Bei längerer Beobachtung stellt man fest, dass man nach einer Zeitspanne manuell nachjustieren kann um der Erdrotation entgegenzuwirken. Deswegen besitzen professionelle azimutale Montierungen an beiden Achsen Schneckenradantriebe. Die meisten solcher Schneckenradantriebe sind elektronisch einstellbar, so dass die Erdrotation automatisch kompensiert wird. Dies ist sehr vorteilhaft, da die Computer dem Beobachter die mühsame Arbeit der Umstellung beider Achsen abnimmt, da er an kleine Antriebmotoren Daten zur Justierung weitergibt. Am Himmel beschreibt der Stern einen Bogen. In Folge dessen kann man sich dann voll und ganz auf die Beobachtung konzentrieren.
Man kann sagen, dass sich ein Stern in Folge der Erdrotation pro Zeitsekunde um 15 Bogensekunden bewegt.
Die Bilder eines azimutal montierten Teleskops leiden unter dem Phänomen der Bildfeldrotation. Das heißt, dass bei der Nachführung eine Kamera der scheinbaren Drehung des Aufnahmefeldes nicht folgen kann. Somit rotiert die Aufnahme um einen gewissen Mittelpunkt. Deswegen verwendet man, wenn man diesen Nachteil ausgleichen will, einen kleinen Motor, der die Kamera entsprechend mitdreht.
Alle modernen professionellen Großteleskope sind heutzutage mit azimutalen Gabelmontierungen ausgestattet. Anders sind die Teleskopgewichte von einigen Dutzend bis zu einigen Hundert Tonnen mechanisch nicht mehr handhabbar. An solche Montierungen werden enorme Genauigkeitsanforderungen gestellt. Bei Bildauflösungen die heute - in Zusammenarbeit mit entsprechender adaptiver Optik im 1/100 Bogensekundenbereich liegt - dürfen sich der Teleskoptubus oder die Achsen der Mechanik in diesem Auflösungsbereich nicht verbiegen oder verwinden. Der mechanische und der elektronische Steueraufwand der hier betrieben wird, ist oft an der Grenze des technisch Machbaren.
III. Parallaktische Montierung
Es handelt sich dabei um zweiachsige Montierungen, bei denen eine Achse parallel (deshalb parallaktisch) zur Erdachse ausgerichtet ist. Eine zweite Achse, die Deklinationsachse, ist orthogonal zur Stundenachse angeordnet. Das ermöglicht das Schwenken der Teleskopöffnung von Pol zu Pol.
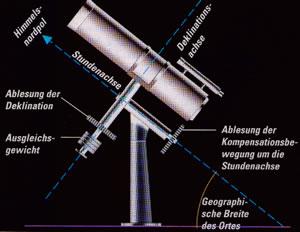
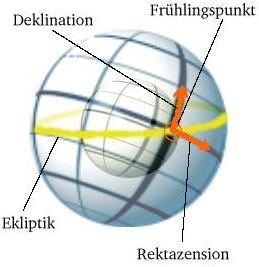Deklination = Die Deklination wird in der Astronomie als eine Koordinate bei der Positionsangabe von Himmelsobjekten verwendet. Sie entspricht der Projektion der Breitenkreise der Erde auf eine (imaginäre) Himmelskugel. Die Deklination gibt somit den Winkelabstand eines Objektes vom Himmelsäquator an. Werte nördlich des Äquators sind positiv, Werte südlich davon negativ
Rektaszension = In der Astronomie ist Rektaszension (lat.: "gerade Aufsteigung") die Entsprechung der geographischen Längenkreise auf der (imaginären) Himmelskugel. Als Nullpunkt der Rektaszension dient dabei der Frühlingspunkt. Die Rektaszension, die bei der Positionsangabe von Himmelsobjekten verwendet wird, wird von Norden aus betrachtet im Gegenuhrzeigersinn gemessen
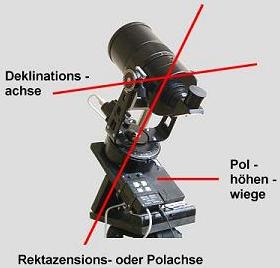Man kann eigentlich sagen, dass die parallaktische Montierung im Prinzip nichts anderes ist, als eine azimutale Montierung. Jedoch ist die azimutale Drehachse unter dem Winkel des Himmelspols und in ihrer Richtung genau Nord-Süd aufgestellt. Die Drehachse nennt man dann Pol- oder Rektaszensionsachse, die Höhenachse wird zur Deklinationsachse.
Die parallaktische Montierung hat gegenüber der azimutalen Montierung einen großen Vorteil. Und zwar, dass die Erddrehung über die Bewegung nur noch einer Achse - der Rektaszensionsachse - kompensiert werden kann. Außerdem treten keine Bildfeldrotationen mehr auf.
Aber die parallaktische Montierung hat gegenüber der azimutalen auch einen großen Nachteil. Und zwar ist dieser durch ihre Bauweise bedingt, welche die Notwendigkeit eines Gegengewichts zum Ausgleich des Tubusgewichtes erforderlich macht.
Die moderne Computertechnologie macht es möglich, dass man die komplexe und sehr genaue Nachjustierung der Achsen und der Kamera mit Hilfe von Computern steuern kann, somit sind die modernsten Weltraumteleskope alle azimutal montiert, da man bei der parallaktischen Montierung mittlerweile an eine Grenze des technisch Machbaren gestoßen ist, was das Ausgleichgewicht und die damit verbundene Problematik bei der Nachjustierung betrifft.
Bilder großer parallaktischer Montierungen:
